
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(k\in Z\)
a.
\(cos\left(x-2\right)=\dfrac{2}{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=arccos\left(\dfrac{2}{5}\right)+k2\pi\\x-2=-arccos\left(\dfrac{2}{5}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2+arccos\left(\dfrac{2}{5}\right)+k2\pi\\x=2-arcos\left(\dfrac{2}{5}\right)+k2\pi\end{matrix}\right.\)
d.
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\cosx=3>1\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
f.
\(\Leftrightarrow cosx=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2\pi}{3}+k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
h.
\(cos\left(3x+10^0\right)=-1\)
\(\Leftrightarrow3x+10^0=180^0+k360^0\)
\(\Leftrightarrow3x=170^0+k360^0\)
\(\Leftrightarrow x=\dfrac{1}{3}.170^0+k120^0\)
j.
\(cos\left[cos\left(x+2\right)\right]=1\)
\(\Leftrightarrow cos\left(x+2\right)=k2\pi\)
Do \(-1\le cos\left(x+2\right)\le1\Rightarrow-1\le k2\pi\le1\)
\(\Rightarrow k=0\)
\(\Rightarrow cos\left(x+2\right)=0\)
\(\Rightarrow x+2=\dfrac{\pi}{2}+n\pi\)
\(\Rightarrow x=-2+\dfrac{\pi}{2}+n\pi\)

\(cos^2x=\dfrac{1}{2}\Leftrightarrow2cos^2x-1=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)



b) `sin^2 3x=1`
`<=> (1-cos6x)/2=1`
`<=> 1-cos6x=2`
`<=> cos6x=-1`
`<=> 6x=π +k2π`
`<=>x=π/6 +k π/3 ( k \in ZZ)`
c) `tan^2 2x=3`
`<=> (1-cos4x)/(1+cos4x)=3`
`<=> 1-cos4x=3+3cos4x`
`<=>cos4x = -1/2`
`<=>4x= \pm (2π)/3 +k2π`
`<=>x = \pm π/6 + k π/2 (k \in ZZ)`

Không biết bạn nhận được nguồn tin từ mới nào mà cho là không có giải vậy nhỉ? Hay là bạn chưa bao giờ được nhận nên nói vậy? Anh hùng bàn phím bay giờ cũng phải chịu trách nhiệm trước pháp luật đấy bạn nhé!
không đăng câu hỏi linh tinh
100% không có giải
lợi dụng đó mọi người đừng tin

3.
\(u_2=\dfrac{1}{2-u_1}=\dfrac{1}{2-\dfrac{1}{2}}=\dfrac{2}{3}\)
\(u_3=\dfrac{1}{2-u_2}=\dfrac{1}{2-\dfrac{2}{3}}=\dfrac{3}{4}\)
\(u_4=\dfrac{1}{2-\dfrac{3}{4}}=\dfrac{4}{5}\)
4.
\(u_1=\dfrac{2^{1+1}+1}{2^1}=\dfrac{5}{2}\)
\(u_3=\dfrac{2^4+1}{2^3}=\dfrac{17}{8}\)
\(u_5=\dfrac{2^6+1}{2^5}=\dfrac{65}{32}\)
5. Đề bị khuất


1.
Hàm số xác định khi:
\(\left\{{}\begin{matrix}sinx\ne0\\cosx-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne k2\pi\end{matrix}\right.\Leftrightarrow x\ne k\pi\)
2.
Hàm số xác định khi:
\(cosx\ne-1\Leftrightarrow x\ne\pi+k2\pi\)
3.
\(cosx+1\ge0\Rightarrow\) Hàm số xác định với mọi x
4.
Hàm số xác định khi:
\(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
5.
Hàm số xác định khi:
\(sin^2x-cos^2x\ne0\Leftrightarrow-cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
6.
Hàm số xác định khi:
\(cos3x-cosx\ne0\Leftrightarrow cos3x\ne cosx\Leftrightarrow3x\ne\pm x+k2\pi\Leftrightarrow\left[{}\begin{matrix}x\ne k\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)
\(sin^2x-cos^2x\ne0\Leftrightarrow-cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
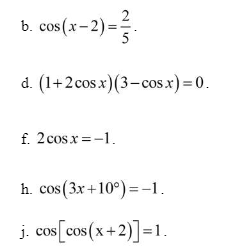




 Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ