Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Điều kiện x ≤ 2.
Viết 2 = ta có log8(4- 2x) ≥
⇔ 4- 2x ≥ 64 ⇔ x ≤ -30.
b) b) >
⇔ 0 < 3x - 5 < x + 1 ⇔
< x < 3.
c) Điều kiện: x > 2. Chú ý rằng
log5(x- 2) = = -log0,2(x- 2), nên bất phương trình đã cho tương đương với
log0,2x + log0,2(x- 2) < log0,23 ⇔ log0,2 x(x- 2) < log0,23 ⇔ x (x - 2) > 3 ⇔
x2- 2x – 3 > 0 ⇔ (x - 3) (x+ 1) > 0 ⇔ x - 3 > 0 ⇔ x > 3 (do x > 2).
d) Đặt t = log3x ta được bất phương trình
t2 – 5t + 6 ≤ 0 ⇔ 2 ≤ t ≤ 3. Trở ại biến cũ ta được 2 ≤ log3x ≤3 ⇔ ≤ log3x ≤
⇔ 9 ≤ x ≤ 27.
Xin lỗi anh soái ca j j đó, nhưng e chưa học ạ ![]()

\(z=x+yi\Rightarrow\left(x+1\right)^2+\left(y+1\right)^2=x^2+y^2\)
\(\Rightarrow x+y+1=0\Rightarrow\) tập hợp z là đường thẳng d: \(x+y+1=0\)
\(P=\left|\left(z-4-5i\right)-\left(w-3-4i\right)\right|\ge\left|\left|z-4-5i\right|-\left|w-3-4i\right|\right|=\left|\left|z-4-5i\right|-1\right|\)
Gọi M là điểm biểu diễn z và \(A\left(4;5\right)\Rightarrow\left|z-4-5i\right|=AM\)
\(AM_{min}=d\left(A;d\right)=\dfrac{\left|4+5+1\right|}{\sqrt{1^2+1^2}}=5\sqrt{2}\)
\(\Rightarrow P\ge\left|5\sqrt{2}-1\right|=5\sqrt{2}-1\)

1) Chọn B
\(\left(z+i\right)^2+3\left(z^2+3zi+2i^2\right)+2\left(z^2+4zi+4i^2\right)=0\\ \Leftrightarrow\left(z+i\right)^2+3\left(z+i\right)\left(z+2i\right)+2\left(z+2i\right)^2=0\\ \Leftrightarrow\left(2z+3i\right)\left(3z+5i\right)=0\)
\(\Rightarrow\left\{\begin{matrix}z_1=-3i:2\\z_2=-5i:3\end{matrix}\right.\)
Vậy \(2z_1+3z_2=2\left(\frac{-3i}{2}\right)+3\left(\frac{-5i}{3}\right)=-8i\)
2) Chọn D
\(\Delta=\left(4-i\right)^2-4\left(5+i\right)=-5-12i\)
Ta có: \(\Delta=\left(2-3i\right)^2\Rightarrow\sqrt{\Delta}=\pm\left(2-3i\right)\)
Nghiệm của pt là:
\(z=\frac{4-i\pm\sqrt{\Delta}}{2}=\frac{4-i\pm\left(2-3i\right)}{2} \)
\(\Rightarrow\left[\begin{matrix}z=3-2i\\z=1+i\end{matrix}\right.\)
Vì \(\left|z_1\right|< \left|z_2\right|\Rightarrow\left\{\begin{matrix}z_1=1+i\\z_2=3-2i\end{matrix}\right.\)
Vậy \(\left|z_1-2z_2\right|=\left|i+1-6+4i\right|=5\sqrt{2}\)

a) =
=
b) =
=
=
. ( Với điều kiện b # 1)
c) \(\dfrac{a^{\dfrac{1}{3}}b^{-\dfrac{1}{3}-}a^{-\dfrac{1}{3}}b^{\dfrac{1}{3}}}{\sqrt[3]{a^2}-\sqrt[3]{b^2}}\)= =
=
( với điều kiện a#b).
d) \(\dfrac{a^{\dfrac{1}{3}}\sqrt{b}+b^{\dfrac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}\) = =
=
=

Đặt \(A=\frac{x+y+z}{3}+\frac{2016}{\sqrt[3]{xyz}}\)
- Tìm giá trị nhỏ nhất :
Áp dụng bđt Cauchy : \(A=\frac{x+y+z}{3}+\frac{2016}{\sqrt[3]{xyz}}\ge\frac{3.\sqrt[3]{xyz}}{3}+\frac{2016}{\sqrt[3]{xyz}}\)
\(\Rightarrow A\ge\sqrt[3]{xyz}+\frac{2016}{\sqrt[3]{xyz}}\ge2\sqrt{\sqrt[3]{xyz}.\frac{2016}{\sqrt[3]{xyz}}}\)
\(\Rightarrow A\ge2\sqrt{2016}=24\sqrt{14}\) .
Dấu "=" xảy ra khi và chỉ khi \(\begin{cases}x=y=z\\\sqrt[3]{xyz}=\frac{2016}{\sqrt[3]{xyz}}\end{cases}\) \(\Leftrightarrow x=y=z=12\sqrt{14}\)
Vậy A đạt giá trị nhỏ nhất bằng \(24\sqrt{14}\) tại \(x=y=z=12\sqrt{14}\)

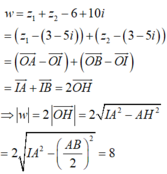

Bài này bạn đã đăng rồi.