Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1
a) \(BC=125\Rightarrow BC^2=15625\)
\(\frac{AB}{AC}=\frac{3}{4}\Rightarrow\frac{AB}{3}=\frac{AC}{4}\)từ đây ta có \(\frac{AB^2}{9}=\frac{AC^2}{16}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có
\(\frac{AB^2}{9}=\frac{AC^2}{16}=\frac{AB^2+AC^2}{25}=\frac{BC^2}{25}=\frac{15625}{25}=625\)
\(\frac{AB^2}{9}=625\Rightarrow AB=75\)
\(\frac{AC^2}{16}=625\Rightarrow AC=100\)
Áp dụng hệ thức lượng trong tam giác vuông ta có
\(AB^2=BH\cdot BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{5625}{125}=45\)
\(AC^2=CH\cdot BC\Rightarrow CH=\frac{AC^2}{BC}=\frac{10000}{125}=80\)
b.c) làm tương tự cũng áp dụng HTL trong tam giác vuông
Bài 2
Hình bạn tự vẽ
Ta có \(EH\\ AC\left(EH\perp AB;AC\perp AB\right)\Rightarrow\frac{BE}{AB}=\frac{BH}{BC}\Rightarrow BE=\frac{AB\cdot BH}{BC}\Rightarrow BE^2=\frac{AB^2\cdot BH^2}{BC^2}\)
\(\Leftrightarrow BE^2=\frac{BH\cdot BC\cdot BH^2}{BC^2}=BH^3\)
Bài 3 Đề bài này không đủ dữ kiện tính S của ABC

Bn tự vẽ hình nhé...
a)
AB⊥CD (GT) => CIB =90 độ (1)
AEB=90độ ( góc nt chắn nữa dg tròn) (2)
Từ (1)và(2) tứ giác BEFI nội tiếp
b)
Xét ΔAFC và Δ ACE có
A( góc chung)
C=E( vì 2 góc cùng chắn 2 cung AC và AD bằng nhau)
=>ΔAFC∼Δ ACE
=> AC/AE=AF/AC
=> AE.AF=AC2

hai cạnh góc vuông đó có độ dài là (8cm)và (6cm)
mình nghĩ như vậy nếu sai bạn thông cảm nha !!!
chúc bạn học tốt
Gọi 2 cạch góc vuông của tam giác lần lượt là a,b :
Ta có : Hai cạch góc vuông hơn kém nhau 2 cm
=> a - b = 2 ( 1 )
Áp dụng định lý pi - ta - go vào tam giác ta đc :
a^2+b^2=10^2(2)
Từ ( 1 ) và ( 2 ) suy ra :
+) a = b+2 thay vào : ( b + 2 )^2 + b^2 = 100
<=> 2b^2 + 4b -96 = 0
=> b=6 ( t/m )hoặc b=8 ( loại )
=> b = 6
=> a =8
Vậy : S = 1/2 .6 . 8 = 24

a) M,N thuộc đường tròn đường kính BC=> Tam giác BMC và tam giác BNC vuông tại M,N
Mà \(\widehat{MAN}=45\Rightarrow\)Tam giác MAC và tam giác NAB vuông cân tại M,N
Khi đó: \(\hept{\begin{cases}OA=OC\\MA=MC\end{cases}\Rightarrow}\)OM là đường trung trực của AC \(\Rightarrow OM\perp AC\)
\(\hept{\begin{cases}OA=OB\\NA=NB\end{cases}\Rightarrow}\)ON là đường trung trực của AB \(\Rightarrow ON\perp AB\)
Vậy O là trực tâm tam giác ABC.
b) \(B,C\in\left(O,OA\right)\Rightarrow OB=OC\)
O thuộc đường tròn đường kính BC=> Tam giác OBC vuông cân tại O \(\Rightarrow\widehat{OBC}=45\)
Tam giác NBA vuông cân tại N \(\Rightarrow\widehat{NBA}=45\)
Vì \(\widehat{OBC}=\widehat{NBA}\) là các góc tại B chắn các cung nhỏ OC và MN của đường tròn đường kính BC \(\Rightarrow MN=OC=BCcos45=\frac{BC}{\sqrt{2}}\)
c) \(\frac{S_{AMN}}{S_{ABC}}=\frac{\frac{1}{2}AM.AN.sin\widehat{MAN}}{\frac{1}{2}AB.AC.sin\widehat{BAC}}=\left(\frac{AM}{AC}\right)\left(\frac{AN}{AB}\right)=cos\widehat{MAN}.cos\widehat{BAC}=cos^245=\frac{1}{2}\)

NA/BA = NC/BC
Vì Tam giác ABC vuông tại A, biết AB=3cm,BC=5cm => AC= 4(cm)
=> NC-NA=4 (cm)
=> NC/BC = NA/BA = ( NC-NA)/(BC-AB) = 2
=> NA= BA*2 =6 (cm)


a) Ta có:
ˆABD=ˆCBD=\(\frac{\widehat{ABC}}{2}\)=120∘: 2=60∘
Từ A kẻ đường thẳng song song với BD cắt CD tại E.
Lại có:
ˆBAE=ˆABD=60∘(so le trong)
ˆCBD=ˆAEB=60∘ (đồng vị)
Suy ra tam giác ABE đều
⇒AB=BE=EA=6(cm)(1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
\(\frac{BC}{CE}\)=\(\frac{DC}{AE}\)⇒BD=\(\frac{BC.AE}{CE}\)=\(\frac{12.6}{18}\)=4(cm)
b) Ta có:
MB=MC=\(\frac{1}{2}\).BC=\(\frac{1}{2}\).12=6(cm)(2)
Từ (1) và (2) suy ra:
BM=AB⇒BM=AB⇒ ∆ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy BD⊥AM
tk mik nha
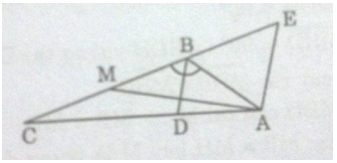
C M B E D A
a) Ta có:
\(\widehat{ABD}=\widehat{CBD}=\frac{\widehat{ABC}}{2}=\frac{120^o}{2}=60^o\)
Từ A kẻ đường thẳng song song với BD cắt CB tại E
Lại có:
\(\widehat{BAE}=\widehat{ABD}=60^o\) ( so le trong )
\(\widehat{CBD}=\widehat{AEB}=60^o\) ( đồng vị )
Suy ra tam giác ABE đều
=> AB = BE = EA = 6 ( cm ) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 ( cm )
Tam giác ACE có AE // BD nên suy ra :
\(\frac{BC}{CE}=\frac{BD}{AE}\)
\(\Rightarrow BD=\frac{BC.AE}{CE}=\frac{12.6}{18}=4\left(cm\right)\)
b) Ta có:
\(MB=MC=\frac{1}{2}.BC=\frac{1}{2}.12=6\left(cm\right)\left(2\right)\)
Từ (1) và (2) suy ra:
BM = AB => Tam giác ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao ( tính chất tam giác cân )
Vậy \(BD\perp AM\)
Bài 1) Vì B = 30°
=》sinB = 1/2 (tính chất )
=》cosB = \(\sqrt{ }\)3/2 ( tính chất )
=》 tanB = \(\sqrt{ }\)3/3( tính chất )
=》 cotB = \(\sqrt{ }\)3( tính chất )
Lại có B + C = 90°
=》 sinB = cosC = 1/2
=》 cosB = sinC = \(\sqrt{ }\)3/2
=》tanB = cotC = \(\sqrt{ }\)3/3
=》cotB = tanC = \(\sqrt{ }\)3
SinA = BC/BC = 1
CosA có thể bằng AB/BC hay AC/BC (loại)
TanA có thể bằng BC/AB hay BC/AC (loại)
CotA có thể bằng AB/BC hay AC/BC (loại)
Bài 2) Vì \(\Delta\)MNP vuông cân tại M
=》 MN = MP = b
Áp dụng định lý Py ta go vào \(\Delta\)ABC có :
NM2 +MP2 = NP2
=》 NP2 =b2 + b2 =2b2
=》NP = \(\sqrt{ }\)2b2
SinN = MP/NP = b/\(\sqrt{ }\)2b2 = \(\sqrt{ }\)2/2
CosN = NM/NP = b/\(\sqrt{ }\)2b2 = \(\sqrt{ }\)2/2
TanN = MP/NM = b/b =1
CotN = NM/MP = b/b = 1
Vì N + P =90°
=》sinN = cosP = \(\sqrt{ }\)2/2
=》cosN = sinP =\(\sqrt{ }\)2/2
=》tanN = cotP = 1
=》cotN = tanP = 1