Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) ˆB3B3^
b) ˆB2B2^
c) 1800 ; là cặp góc trong cùng phía
d) Bằng cặp góc so le trong ˆB2B2^=ˆA4A4^.
a) \(\widehat{A_1}\)\(=\widehat{B_3}\)(vì là cặp góc so le trong)
b)\(\widehat{A_2}\)\(=\widehat{B_2}\)(vì là cặp góc đồng vị)
c)\(\widehat{B_3}\)\(+\widehat{A_4}\)\(=180^0\)(vì là cặp góc trong cùng phía)
d)\(\widehat{A_2}\)\(=\widehat{B_4}\)(vì là cặp góc cùng bằng \(\widehat{A_4}\) )
Ủng hộ mk nhé!!! ^.^
( vì cặp góc trong cùng phía bù sau)
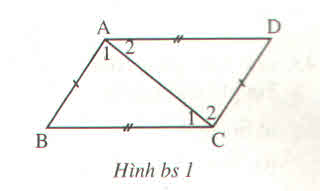
\(\widehat{A}_1=\widehat{C}_2;\widehat{A}_2=\widehat{C}_1;\widehat{B}=\widehat{D}\)
a) Góc xOy và góc .....là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
b) Góc x'Oy và góc xOy' là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
ghi ngắn gọn là ( ghi mỗi đáp án)
a) X'OY'
b) là hai góc đối đỉnh
+) Của cạnh OX' và cạnh OY là tia đối của cạnh OY'
B A C M K H G I
a) Xét hai tam giác MHB và MKC có:
MB = MC (gt)
Góc HMB = góc KMC (đối đỉnh)
MH = MK (gt)
Vậy: tam giác MHB = tam giác MKC (c - g - c)
c) Ta có: AM = MB = MC = \(\dfrac{1}{2}\) BC (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
=> Tam giác MAB cân tại M
=> MH là đường cao đồng thời là đường trung tuyến
hay HB = HA
=> CH là đường trung tuyến ứng với cạnh AB
Hai đường trung tuyến AM và CH cắt nhau tại G
=> G là trọng tâm của tam giác ABC
Mà BI đi qua trọng tâm G (G thuộc BI)
Do đó BI là đường trung tuyến còn lại
hay I là trung điểm của AC (đpcm).
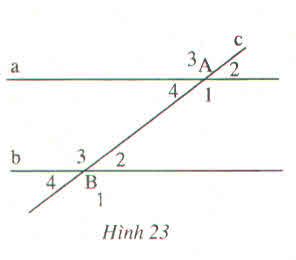
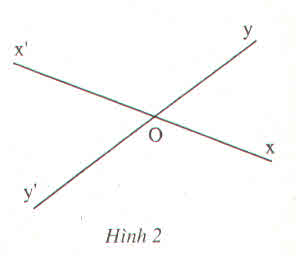
Căn cứ vào hình vẽ, ta điền được như sau: