Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao là tam giác cân, tam giác vuông cân, tam giác đều.

Tam giác có trọng tâm đồng thời là trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh là tam giác đều.

Câu 1:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
DB= DC
=> tam giác ABD = tam giác ACD (2 cạnh góc vuông)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 2:
Chứng minh y chang câu 1
Câu 3:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
BAD = CAD
=> tam giác ABD = tam giác ACD (cạnh góc vuông_ góc nhọn)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 4:
Chứng minh giống hệt câu 3.

bạn tham khảo link này nha:https://hoc24.vn/hoi-dap/tim-kiem?id=137279&q=Ch%E1%BB%A9ng%20minh%20%3A%20trong%20m%E1%BB%99t%20tam%20gi%C3%A1c%20c%C3%A2n%2C%20%C4%91%C6%B0%E1%BB%9Dng%20ph%C3%A2n%20gi%C3%A1c%20xu%E1%BA%A5t%20ph%C3%A1t%20t%E1%BB%AB%20%C4%91%E1%BB%89nh%20%C4%91%E1%BB%93ng%20th%E1%BB%9Di%20l%C3%A0%20%C4%91%C6%B0%E1%BB%9Dng%20trung%20tuy%E1%BA%BFn%20%E1%BB%A9ng%20v%E1%BB%9Bi%20c%E1%BA%A1nh%20%C4%91%C3%A1y.

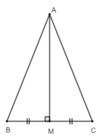
Giả sử Δ A B C có AM là trung tuyến đồng thời là đường trung trực. Ta sẽ chứng minh Δ A B C là tam giác cân. Thật vậy, vì AM là trung tuyến của Δ A B C g t ⇒ B M = M C (tính chất trung tuyến)


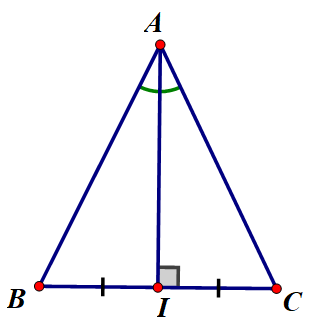
Xét tam giác ABC có AI là đường trung trực vừa là đường phân giác
vì AI là đường trung trực nên AI vuông góc với BC và I là trung điểm cuả BC
xét 2 tam giác vuông ABI và tam giác vuông ACI có;
IA chung
góc BAI=gócCAI (do AI là phân giác)
do đó tam giác BAI =tam giác CAI
suy ra AB=AC (2 cạnh tương ứng)
suy ra tam giác ABC cân tại A (định nghĩa tam giác cân)

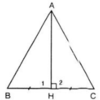
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC, có:
HB = HC
AH: cạnh chung
Nên ∆HAB = ∆HAC (hai cạnh góc vuông)
⇒ AB = AC (hai cạnh tương ứng)
Vậy ∆ABC cân tại A.
Tam giác có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao là tam giác cân, tam giác vuông cân.
Trả lời
Tam giác có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao là tam giác cân, tam giác vuông cân.