Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có x1 = 1 có tần số n1 = 2100 (lớn nhất)
⇒ Mốt của bảng phân bố đã cho là: Mo = 1
b) Trong sản xuất, nhà máy nên ưu tiên cho mẫu số 1

Đáp án A
Ta có:
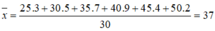
Dựa vào bảng số liệu trên ta thấy giá trị 40 có tần số lớn nhất là 9. Do đó, mốt của mẫu số liệu trên là 40
Giá trị thứ 15,16 của dãy số liệu là 35; 40. Do đó, số trung vị của dãy số liệu là:
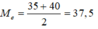

Chọn A.
Bảng phân bố tần số - tần suất
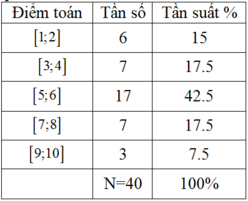
Dựa vào bảng trên ta thấy lớp 3 có tần số và tần suất cao nhất; lớp 5 có tần số; tần suất thấp nhất.
Lớp 2 và 4 có cùng tần số và tần suất.

Chọn C.
Bảng phân bố tần số - tần suất
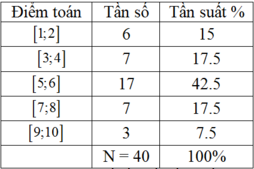
Dựa vào bảng phân bố tần số; tần suất trên ta thấy có 3 lớp có tần suất không bé hơn 17,5% là lớp thứ 2;3 và lớp thứ 4.

Trong bảng phân bố trên, hai giá trị 700 và 900 có cùng tần số lớn nhất là 6. Do đó ta có hai mốt là:
M0(1) = 700; M0(2) = 900.
Ý nghĩa:
+ Số công nhân có tiền lương 700.000đ/tháng và 900.000đ/tháng bằng nhau và chiếm đa số.
+ Tỉ lệ công nhân có mức lương 700 nghìn đồng / tháng và 900 nghìn đồng/ tháng cao hơn tỉ lệ công nhân có các mức lương khác.

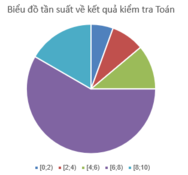
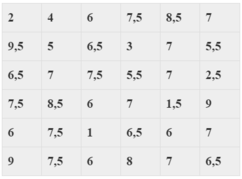
a) Lập bảng phân bố tần số và tần suất ghép lớp ( chính xác đến hàng phần trăm) sử dụng 5 lớp sau: [0;2), [2;4), [4;6), [6;8), [8;10)
| Lớp | Tần số | Tần suất |
|---|---|---|
| [0;2) | 2 | 5,56% |
| [2;4) | 3 | 8,33% |
| [4;6) | 4 | 11,11% |
| [6;8) | 21 | 58,33% |
| [8;10) | 6 | 16,67% |
| N = 36 | 100% |
b) Vẽ biểu đồ tần suất hình quạt thể hiện bảng phân bố ở câu a).

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.
Như vậy tiền lãi có được là L = 3x + 5y (nghìn đồng).
Theo đề bài: Nhóm A cần 2x + 2y máy;
Nhóm B cần 0x + 2y máy;
Nhóm C cần 2x + 4y máy;
Vì số máy tối đa ở nhóm A là 10 máy, nhóm B là 4 máy, nhóm C là 12 máy nên x, y phải thỏa mãn hệ bất phương trình: 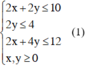
Khi đó bài toán trở thành: trong các nghiệm của hệ bất phương trình (1) thì nghiệm (x = xo; y = yo) nào cho L = 3x + 5y lớn nhất.
Miền nghiệm của hệ bất phương trình (1) là ngũ giác ABCDE kể cả miền trong.
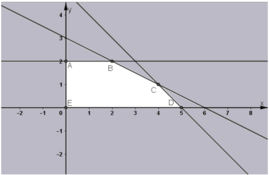
Ta có: L đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác ABCDE.
Tính giá trị của biểu thức L = 3x + 5y tại các đỉnh ta được:
Tại đỉnh A(0;2), L = 10
Tại đỉnh B(2; 2), L = 16
Tại đỉnh C(4; 1), L = 17
Tại đỉnh D(5; 0), L = 15
Tại đỉnh E(0; 0), L = 0.
Do đó, L = 3x + 5y lớn nhất là 17 (nghìn đồng) khi: x = 4; y = 1
Vậy để có tiền lãi cao nhất, cần sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm loại II.

a) Số trung bình của nhóm cá mè thứ nhất:
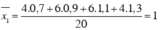
Số trung bình của nhóm cá mè thứ hai:
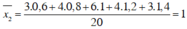
b) Phương sai của bảng phân bố khối lượng của nhóm cá mè thứ 1:
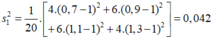
Phương sai của bảng phân bố khối lượng của nhóm cá mè thứ 2:
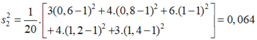
c) Nhận xét: s12 < s22 nên nhóm cá thứ nhất có khối lượng đồng đều hơn.

Bảng phân bố tần số
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân
| Thời gian (phút) | 42 | 44 | 45 | 48 | 50 | 54 | cộng |
| Tần số | 4 | 5 | 20 | 10 | 8 | 3 | 50 |
Bảng phân bố tần suất
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân
| Thời gian (phút) | 42 | 44 | 45 | 48 | 20 | 54 | Cộng |
| Tần suất (%) | 8 | 10 | 40 | 20 | 16 | 6 | 100% |
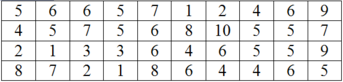
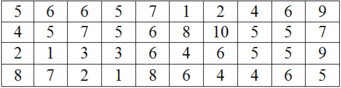

a) Ta có x1 = 1 có tần số n1 = 2100 (lớn nhất)
=> Mốt của bảng phân bố đã cho là: Mo = 1
b) Trong sản xuất, nhà máy nên ưu tiên cho mẫu số 1