Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c; Quãng đường vật rơi của 2s đầu tiên:
![]()
Vậy sau 2s đầu tiên vật còn cách mặt đất:
![]()
d; Thời gian để vật đạt được vận tốc 40m/s là:


Giải:
a; Áp dụng công thức h = 1 2 g t 2 ⇒ t = 2 h g = 2.1280 10 = 16 s
b; Áp dụng công thức v = g t = 10.16 = 160 ( m / s )
c; Quãng đường vật rơi của 2s đầu tiên h 1 = 1 2 g . t 1 2 = 1 2 .10.2 2 = 20 m
Vậy sau 2s đầu tiên vật còn cách mặt đất h 2 = h − h 1 = 1280 − 20 = 1260 m
d; Thời gian để vật đạt được vận tốc 40m/s là
v = g t ⇒ 40 = 10 t ⇒ t = 4 s
Quãng đường vật rơi trong 4s đầu là:
h 3 = 1 2 g t 3 4 = 1 2 .10.4 4 = 80 m
Vật cách mặt đấy là Δ h = h − h 3 = 1280 − 80 = 1200 m
Vậy còn 16 – 4 = 12s vật chạm đất

a) Thời gian vật rơi chạm đất là:
\(S=\dfrac{1}{2}gt^2\Rightarrow t=\sqrt{\dfrac{2S}{g}}=\sqrt{\dfrac{2.70}{9,8}}\approx3,78\left(s\right)\)
b) Quãng được vật rơi trong giây thứ ba là:
\(S=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-1\right)^2=\dfrac{1}{2}.9,8.3^2-\dfrac{1}{2}.9,8.\left(3-1\right)^2=24,5\left(m\right)\)

a,\(\Rightarrow v^2=2gh\Rightarrow h=\dfrac{v^2}{2g}=\dfrac{20^2}{2.10}=20m\)
\(b,\Rightarrow v=gt\Rightarrow t=\dfrac{v}{g}=\dfrac{20}{10}=2s\)
c,\(\Rightarrow t=\sqrt{\dfrac{2,S'}{g}}=\sqrt[]{\dfrac{2.15}{10}}=\sqrt{3}\left(s\right)\)

a. \(v^2=2gh\Rightarrow h=\dfrac{v^2}{2g}=\dfrac{20^2}{2.10}=20\left(m\right)\)
b. \(v=gt\Rightarrow t=\dfrac{v}{g}=\dfrac{20}{10}=2\left(s\right)\)
c. \(v'=gt'\Rightarrow t'=\dfrac{v'}{g}=\dfrac{10}{10}=1\left(s\right)\)
\(h'=\dfrac{1}{2}gt^2=\dfrac{1}{2}.10.1^2=5\left(m\right)\)
\(\Rightarrow\Delta h=h-h'=20-5=15\left(m\right)\)
Vậy còn: 2 - 1 = 1(s) vật chạm đất.

Quãng đường vật rơi nửa thời gian đầu:
![]()
Quãng đường vật rơi nửa thời gian cuối
![]()
Quãng đường vật rơi: h = h 1 + h 2
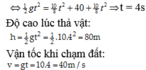

a) Thời gian vật rơi: \(t=\sqrt{\dfrac{2S}{g}}=\sqrt{\dfrac{2\cdot54,6}{9,8}}=\dfrac{\sqrt{546}}{7}=3,34s\)
b) Vận tốc vật khi chạm đất: \(v=gt=\dfrac{7\sqrt{546}}{5}=32,71\)m/s
c) Thời gian vật rơi nửa quãng đường:
\(\dfrac{1}{2}S=\dfrac{1}{2}gt^2\Rightarrow t=\sqrt{\dfrac{S}{g}}=\sqrt{\dfrac{54,6}{9,8}}=\dfrac{\sqrt{273}}{7}=2,36s\)