Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
giup mình nha
Nước ngọt loại 1: pha được tối đa 6 lít nếu chỉ pha loại này ; nước ngọt loại 2: pha được tối đa 7 lít nếu chỉ pha loại này (dựa trên lượng sử dụng tối đa của hương liệu)
Vì 1 lít nước ngọt loại 1 được tính điểm cao hơn loại 2 \(\Rightarrow\)Chọn pha nước ngọt loại 1 trước
6 lít là max của nước ngọt loại 1 \(\Rightarrow\) Pha 5 lít nước ngọt loại 1 \(\Rightarrow\)Tốn 50 gam đường, 5 lít nước, 20 gam hương liệu
Còn được pha 160 gam đường, 4 lít nước, 4 gam hương liệu \(\Rightarrow\)Pha 4 lít nước ngọt loại 2.
\(\Rightarrow\)Số điểm thưởng cao nhất: 5 lít loại 1 = 5.80 =400 ; 4 lít loại 2 = 4.60 = 240 ; 400 + 240 = 640 (điềm)
Tham khảo:
Để pha x lít nước cam loại I cần 30x g bột cam,
Để pha y lít nước cam loại II cần 20y g bột cam,
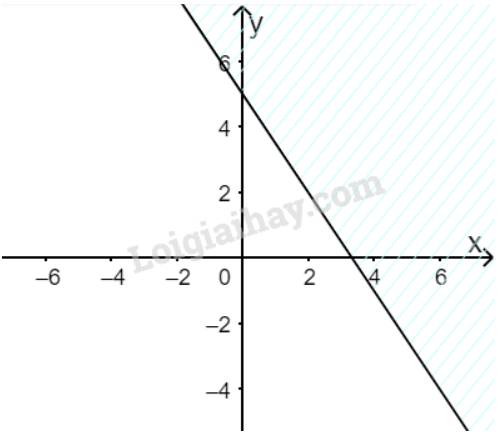
Vì Cúc chỉ có thể dùng không quá 100 gam bột cam nên ta có bất phương trình \(30x + 20y \le 100\)
\( \Leftrightarrow 3x + 2y - 10 \le 0\)
Vẽ đường thẳng \(\Delta :3x + 2y - 10 = 0\) đi qua hai điểm \(A(0;5)\) và \(B\left( {2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(3.0 + 2.0 - 10 = - 10 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
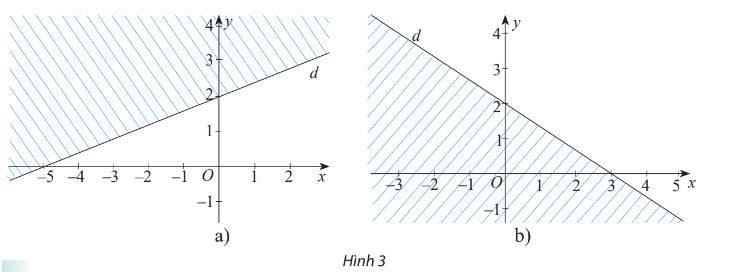
Gọi phương trình đường thẳng \(d:ax + by + c = 0\)
a) Từ hình a) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B( - 5;0)\)
\( \Rightarrow \left\{ \begin{array}{l}b.2 + c = 0\\ - 5a + c = 0\end{array} \right. \Rightarrow c = 5a = - 2b\)
Chọn \(a = 2 \Rightarrow b = - 5;c = 10\) và \(d:2x - 5y + 10 = 0\)
Điểm O (0;0) thuộc miền nghiệm và \(2.0 - 5.0 + 10 = 10 > 0\)
Vậy bất phương trình cần tìm là \(2x - 5y + 10 > 0\)
b) Từ hình b) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B(3;0)\)
\( \Rightarrow \left\{ \begin{array}{l}2b + c = 0\\3a + c = 0\end{array} \right. \Rightarrow - c = 3a = 2b\)
Chọn \(a = 2 \Rightarrow b = 3;c = - 6\) và \(d:2x + 3y - 6 = 0\)
Điểm O (0;0) không thuộc miền nghiệm và \(2.0 + 3.0 - 6 = - 6 < 0\)
Vậy bất phương trình cần tìm là \(2x + 3y - 6 > 0\)
Gọi t1 (giờ) là thời gian người thứ nhất sơn xong bức tường,
t2 (giờ) là thời gian người thứ hai sơn xong bức tường.
(Điều kiện: t1 > 0; t2 > 0)
+ Trong một giờ:
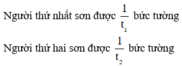
+ Người thứ nhất làm trong 7 giờ và người thứ hai làm trong 4 giờ thì họ sơn được 5/9 bức tường nên ta có: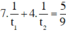 
+ Sau đó họ cùng làm việc với nhau trong 4 giờ nữa, nghĩa là người thứ nhất làm trong 7 + 4 = 11 giờ và người thứ hai làm trong 4 + 4 = 8 giờ.
Khi đó họ còn 1/18 bức tường chưa sơn nghĩa là họ đã sơn được 17/18 bức tường.
Ta có phương trình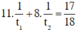 
Ta có hệ phương trình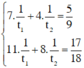 
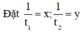, khi đó hệ phương trình trở thành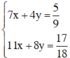 
Giải hệ phương trình trên ta được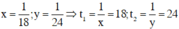 
Vậy nếu mỗi người làm riêng thì người thứ nhất sơn xong bức tường trong 18 giờ, người thứ hai sơn xong bức tường trong 24 giờ.
Gọi x (giờ), y(giờ) là thời gian để công nhân thứ nhất, thứ hai làm riêng để sơn xong bức tường.
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{7}{x}+\dfrac{4}{y}=\dfrac{5}{9}\\\dfrac{4}{x}+\dfrac{4}{y}=1-\dfrac{5}{9}-\dfrac{1}{18}=\dfrac{7}{18}\end{matrix}\right.\)
Giải hệ phương trình trên ta được: \(\dfrac{1}{x}=\dfrac{1}{18};\dfrac{1}{y}=\dfrac{1}{24}\)
Suy ra x = 18, y = 24.
Vậy mỗi người làm riêng, theo thứ tự, thời gian sơn xong bức tường là 18 giờ và 24 giờ.
lớp 6