QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
B
1
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
Gợi ý ví dụ trong thực tiễn minh họa hình ảnh hai mặt phẳng song song: các mặt sàn của ngôi nhà; các mặt bậc cầu thang; mặt bàn và nền nhà.
B
1
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
Những ví dụ trong thực tiễn minh hoạ hình ảnh hai mặt phẳng vuông góc là: Mặt tường vuông góc với sàn nhà, mặt ngang vuông góc với mặt đứng của bậc thang,…
22 tháng 7 2023
a: Các tấm pin năng lượng mặt trời song song với nhau
b: Các bức tường đối diện nhau của toà nhà song song với nhau
Các ví dụ khác: Các bậc cầu thang, mặt bàn và mặt phẳng sàn nhà
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Cái nắm cửa tủ cho ta hình ảnh về một điểm thuộc một mặt phẳng.
PT
1
CM
23 tháng 5 2019
Hàm số cho bằng bảng
Ví dụ:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 | 9 |
- Hàm số cho bằng công thức:
Ví dụ:
B
1
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
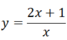
Ta có (MNPQ) // (ABCD) (chứng minh ở Ví dụ 2)
Vì vậy giao tuyến của (EMQ) với hai mặt phẳng (MNPQ) và (ABCD) song song với nhau
Trong mặt phẳng (EMQ), qua E vẽ đường thẳng ET // MQ (T thuộc CD)
Như vậy, đường thẳng ET là giao tuyến của (EMQ) và (ABCD).
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
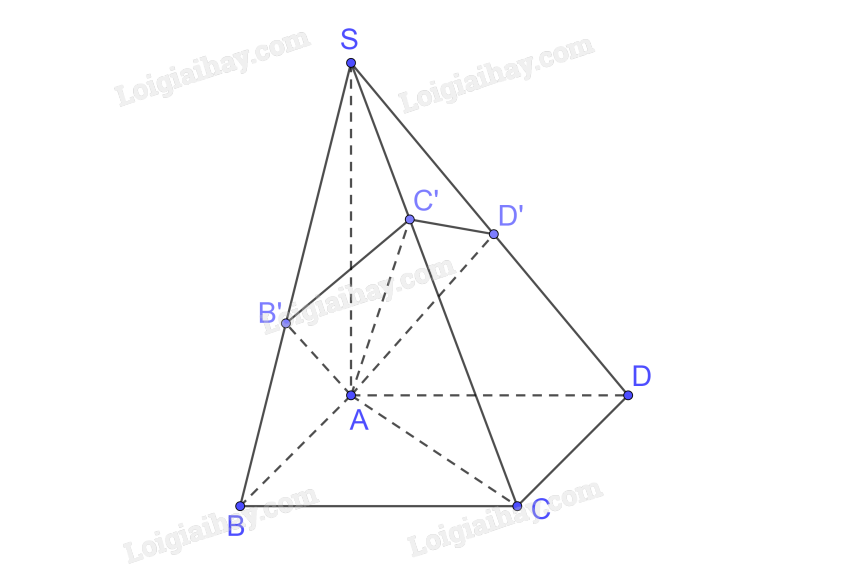
a) Từ ví dụ 3b ta có AB’, AC’ cùng đi qua A và vuông góc với SC
\( \Rightarrow SC \bot \left( {AB'C'D'} \right),SC \subset \left( {SAC} \right) \Rightarrow \left( {AB'C'D'} \right) \bot \left( {SAC} \right)\)
Ta có \(SA \bot \left( {ABCD} \right),SA \subset \left( {SAC} \right) \Rightarrow \left( {ABCD} \right) \bot \left( {SAC} \right)\)
Do đó các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC).
b) Vì (AB'C'D') và (ABCD) cùng vuông góc với (SAC) nên giao tuyến của hai mặt phẳng (AB'C'D') và (ABCD) vuông góc với (SAC)
Vậy giao tuyển của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.
Trong thực tiễn có nhiều ví dụ minh họa cho mặt phẳng. Chẳng hạn: tấm gương phẳng, mặt bàn, mặt bảng… Cho ta hình ảnh một phần mặt phẳng trong không gian