Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a)\frac{2x^3-7x^2-12x+45}{3x^3-19x^2+33x-9}=\frac{(x-3)^2(2x+5)}{(3x-1)(x-3)^2}(ĐK:x\ne3,x\ne\frac{1}{3})\)
\(=\frac{2x+5}{3x-1}\)
Còn bài b bạn tự làm nhé
Điều kiện: \(x\ne\left\{-1;-2;-5\right\}\)
\(\frac{x^3+x^2-4x-4}{x^3+8x^2+17x+10}=\frac{x^2\left(x+1\right)-4\left(x+1\right)}{x^2\left(x+1\right)+7x\left(x+1\right)+10\left(x+1\right)}\)
\(=\frac{\left(x+1\right)\left(x^2-4\right)}{\left(x+1\right)\left(x^2+7x+10\right)}\)
\(=\frac{\left(x+1\right)\left(x-2\right)\left(x+2\right)}{\left(x+1\right)\left[x\left(x+2\right)+5\left(x+2\right)\right]}\)
\(=\frac{\left(x+1\right)\left(x-2\right)\left(x+2\right)}{\left(x+1\right)\left(x+2\right)\left(x+5\right)}=\frac{x-2}{x+5}\)
Điều kiện: \(x\ne\left\{3;\frac{1}{3}\right\}\)
\(\frac{2x^3-7x^2-12x+45}{3x^3-19x^2+33x-9}=\frac{2x^3-6x^2-x^2+3x-15x+45}{3x^3-9x^2-10x^2+30x+3x-9}\)
\(=\frac{2x^2\left(x-3\right)-x\left(x-3\right)-15\left(x-3\right)}{3x^2\left(x-3\right)-10x\left(x-3\right)+3\left(x-3\right)}\)
\(=\frac{\left(x-3\right)\left(2x^2-x-15\right)}{\left(x-3\right)\left(3x^2-10x+3\right)}\)
\(=\frac{2x^2-x-15}{3x^2-10x+3}=\frac{2x\left(x-3\right)+5\left(x-3\right)}{3x\left(x-3\right)-\left(x-3\right)}\)
\(=\frac{\left(2x+5\right)\left(x-3\right)}{\left(3x-1\right)\left(x-3\right)}=\frac{2x+5}{3x-1}\)

Qui tắc rút gọn một phân thức đại số.
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
- Chia cả tử và mẫu cho nhân tử chung đó.
Rút gọn:
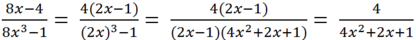

a)\(\dfrac{3x^2-12x+12}{x^4-8x}=\dfrac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x^3-2^3\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)

Không ai trả lời buồn quá .
\(\frac{3x^2-12x+12}{x^4-8x}\)
\(=\frac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}\)
\(=\frac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+2^2\right)}\)
\(=\frac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)

a) \(\dfrac{36\left(x-2\right)^3}{32-16x}=\dfrac{36\left(x-2\right)^3}{16\left(2-x\right)}=\dfrac{36\left(x-2\right)^3}{-16\left(x-2\right)}\)\(=\dfrac{36\left(x-2\right)^3:4\left(x-2\right)}{-16\left(x-2\right):4\left(x-2\right)}\)\(=\dfrac{9\left(x-2\right)^2}{-4}\)
b) \(\dfrac{x^2-xy}{5y^2-5xy}=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{x\left(x-y\right)}{-5y\left(x-y\right)}\)\(=\dfrac{x}{-5y}\)

Ta có \(\frac{32x-8x^2+2x^3}{x^3+64}=\frac{x\left(32-8x+2x^2\right)}{\left(x+4\right)\left(x^2-4x+16\right)}=\frac{2x\left(x^2-4x+16\right)}{\left(x+4\right)\left(x^2-4x+16\right)}=\frac{2x}{x+4}\)
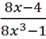
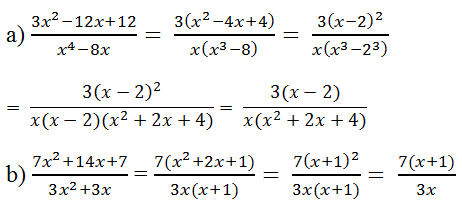

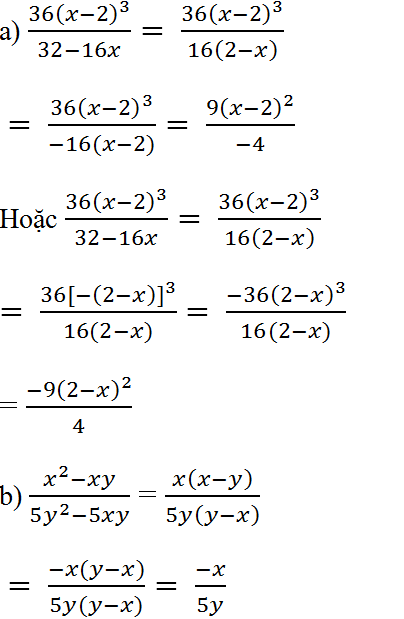
Muốn rút gọn phân thức đại số ta có thể :
+ Phân tích tử và mẫu thành nhân tử ( nếu cần ) để tìm nhân tử chung.
+ Chia cả tử và mẫu cho nhân tử chung.
Rút gọn phân thức :
\(\dfrac{8x-4}{8x^3-1}\)\(=\dfrac{4\left(2x-1\right)}{2x^3-1}\)\(=\dfrac{4\left(2x-1\right)}{\left(2x-1\right)\left(2x^2+2x+1\right)}\)\(=\dfrac{4}{4x^2+2x+1}\)
*Quy tắc rút gọn một phân thức đại số là:
-Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
-Chia cả tử và mẫu cho nhân tử chung.
*Bài tập:
\(\dfrac{8x-4}{8x^3-1}=\dfrac{4\left(2x-1\right)}{\left(2x-1\right)\left(x^2+x+1\right)}=\dfrac{4}{x^2+x+1}\)