Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên đường tròn lượng giác,từ A(1,0) vẽ tiếp tuyến t’At với đường tròn lượng giác.
Từ B(0,1) vẽ tiếp tuyến s’Bs với đường tròn lượng giác .
Cho cung lượng giác AM có số đo α (α ≠ π/2 + kπ ). Gọi T là giao điểm của OM với trục t’At.
Gọi S là giao điểm của OM và trục s’Bs.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm T trên trục tan. Do đó
tan(α + kπ) = tanα.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm S trên trục cot. Do đó
cot(α + kπ) = cotα.

Chọn C.
Ta có tan α – cotα = 1

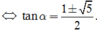
Do ![]() suy ra tanα < 0 nên
suy ra tanα < 0 nên
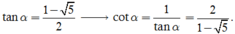
Thay
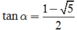 và
và 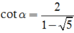
vào P ta được
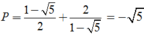

Vì \(\dfrac{\pi}{2}< \alpha< \pi\) \(\Rightarrow\) cos \(\alpha\) < 0
\(\Rightarrow\) cos \(\alpha\) = \(-\sqrt{1-sin^2\alpha}\) = \(-\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\) tan \(\alpha\) = \(\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{2}}{4}\)
\(\Rightarrow\) cot \(\alpha\) = \(\dfrac{1}{tan\alpha}\) = \(-2\sqrt{2}\)
Chúc bn học tốt!

+) Định nghĩa của sin α; cos α
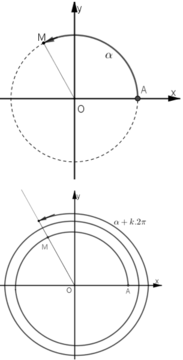
Trên đường tròn lượng giác, xét cung AM có số đo α
Gọi H và K lần lượt là hình chiếu của M trên trục Ox, Oy.
Tung độ y = OK¯ của điểm M được gọi là sin của α : sin α = OK¯
Hoành độ x = OH¯ của điểm M được gọi là cos của α : cos α = OH¯
Trên đường tròn lượng giác trong mặt phẳng Oxy, lấy điểm A (1; 0) làm gốc.
Khi đó các cung có số đo hơn kém nhau một bội của 2π có điểm cuối trùng nhau.
Giả sử cung α có điểm cuối là M(x; y)
Khi đó với mọi k ∈ Z thì cung α + k2π cũng có điểm cuối là M.
sin α = y, sin (α + k2π) = y nên sin(α + k2π) = sinα
cos α = x, cos(α + k2π) = x nên cos(α + k2π) = cosα

Chọn B.
Ta có P = tan3α + cot3α = (tanα + cotα) 3 - 3tanα.cotα( tanα + cotα)
= 53 - 3.5 = 110
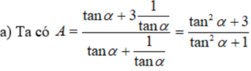
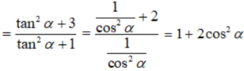

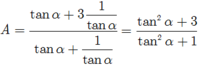
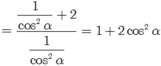
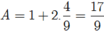
+) Nếu k lẻ: k = 1+2m ; m ∈ Z , ta có: