Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thông cảm , hình ko cho vẽ
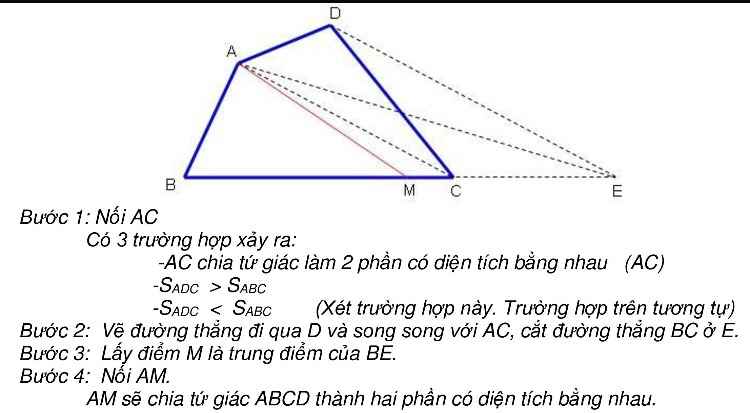
Bước 1 : Nối AC
Có 3 trường học xảy ra :
- AC chia tứ giác làm 2 phần diện tích bằng nhau ( AC)
\(-Sadc>Sabc\)
\(-Sadc< Sabc\)
( Xét trường hợp này trường hợp tương tự )
Bước 2 : Vẽ đường thẳng qua D và song song với AC , cắt đường BC ở E .
Bước 3 : Lấy M đi qua trung điểm của BE
Bước 4 : Nối AM
AM sẽ chia tứ giác ABCD thành hai phần có diện tích bằng nhau

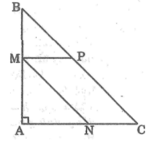
Gọi x (cm) là độ dài đoạn AM.
Điều kiện: 0 < x < 12
Vì ΔABC vuông cân tại A nên ΔBMP vuông cân tại M.
Suy ra MP = MB = AB – AM = 12 – x (cm)
Diện tích hình bình hành MNCP bằng MP.MA = (12 – x)x ( c m 2 )
Theo đề bài, ta có phương trình:
(12 – x)x = 32 ⇔ x 2 – 12x + 32 = 0
∆ ' = - 6 2 – 1.32 = 36 – 32 = 4 > 0
∆ ' = 4 = 2
![]()
Cả hai giá trị của x đều thỏa mãn điều kiện bài toán
Vậy điểm M cách điểm A 8cm hoặc 4cm thì diện tích hình bình hành MNCP bằng 32 c m 2

Áp dụng HTL trong tam giác ABC vuông tại A:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow AB=\sqrt{\dfrac{1}{\dfrac{1}{AH^2}-\dfrac{1}{AC^2}}}=\sqrt{\dfrac{1}{\dfrac{1}{20^2}-\dfrac{1}{35^2}}}\approx24\left(m\right)\)
\(BC^2=AB^2+AC^2\left(Pytago\right)\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+35^2}\approx43\left(m\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.20.43\approx426\left(m^2\right)\)
ny lê song phương là bùi diệu linh đó