Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

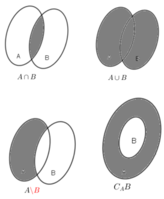
– Giao của hai tập hợp: A ∩ B = {x | x ∈ A và x ∈ B}
– Hợp của hai tập hợp: A ∪ B = {x | x ∈ A hoặc x ∈ B}
– Hiệu của A và B: A \ B = {x | x ∈ A và x ∉ B}
– Phần bù của B trong A: Nếu B ⊂ A thì A \ B gọi là phần bù của B trong A, kí hiệu: CAB.
- Hình minh họa:

Có hai cách cho một tập hợp:
+) Liệt kê các phần tử của tập hợp.
Chẳng hạn: A = {0; 1; 2; 3; 4; 5}
+) Chỉ ra tính chất đặc trưng của tập hợp đó.
Chẳng hạn: A = {\(x \in \mathbb{N}|0 \le x \le 5\)}

Đáp án: B
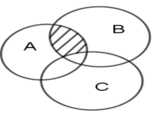
Phần bị gạch là phần thuộc (A ∩ B) nhưng không thuộc C nên phần bị gạch biểu thị cho (A ∩ B) \ C.

Đáp án: B
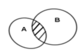
Phần bị gạch là phần chung của A và B, được kí hiệu là A ∩ B.

Đáp án: D
Phần không bị gạch là phần thuộc B nhưng không thuộc A, được kí hiệu là B \ A.

– Tập hợp con: Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói rằng tập hợp A là tập hợp con của tập hợp B.
Kí hiệu: A ⊂ B ⇔ ∀ x ∈ A thì x ∈ B
– Khi A ⊂ B và B ⊂ A ta nói tập hợp A bằng tập hợp B và viết là A = B.
(Hiểu cách khác: Hai tập hợp bằng nhau là hai tập hợp có phần tử giống hệt nhau).

Vì các học sinh tổ I đều là các học sinh lớp 10D nên tập hợp B là tập con của tập hợp A.
Kí hiệu: \(B \subset A\)

A∩B ⇔ ∀x (x∈A và x∈B) (h.1)
A ∪B ⇔ ∀x (x∈A hoặc x∈B) (h.2)
A\B ⇔ ∀x (x∈A và x∉B) (h.3)
Cho A⊂E.CEA = {x/x∈E và x∉A} (h.4)