Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có V=a.b.c với a, b là độ dài hai cạnh đáy, suy ra V'=10a. 10b. c=100abc=100V

Đáp án A
Gọi R, h lần lượt là bán kính và chiều cao của khối trụ ban đầu, khi đó thể tích khối trụ ![]()
Khi bán kính tăng lên 2 lần thì thể tích khối trụ mới là ![]() .
.

Đáp án C
Phương pháp:
Thể tích khối chóp V = 1 3 S h
Cách giải:
Thể tích khối chóp ban đầu: V = 1 3 S h
Theo đề bài, ta có:
![]()
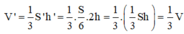
=> Thể tích khối chóp đó giảm 3 lần.

\(S=4\pi R^2\) ; \(S'=4\pi R'^2\)
\(S'=27S\Rightarrow R'^2=27R^2\Rightarrow R'=3\sqrt{3}R\)
\(\Rightarrow V'=\dfrac{4}{3}\pi R'^3=\dfrac{4}{3}\pi\left(3\sqrt{3}R\right)^3=81\sqrt{3}V\)
Thể tích tăng \(81\sqrt{3}\) lần
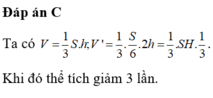
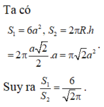


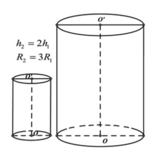
Đáp án A
Giả sử khối hộp chữ nhật có ba kích thước là a, b, c và thể tích ban đầu V₁ = abc. Nếu tăng mỗi kích thước lên 4 lần thì thể tích khối hộp sau khi tăng là V₂ = 4a. 4b. 4c = 64abc. Điều đó có nghĩa thể tích khối hộp tăng lên 64 lần.