Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
Gọi số học sinh khối 6,7,8,9 lần lượt là a,b,c,d
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{16}=\dfrac{b}{24}=\dfrac{c}{30}=\dfrac{d}{35}=\dfrac{a+b+c+d}{16+24+30+35}=\dfrac{210}{105}=2\)
Do đó: a=32; b=48; c=60; d=70

Bài 2:
a: Đó là gốc tọa độ
b: Điểm đó nằm trên trục tung
c: Điểm đó nằm trên trục hoành
Bài 1:
a: Ta có: \(x\cdot\dfrac{4}{5}+\dfrac{1}{6}=\dfrac{1}{2}\)
\(\Leftrightarrow x\cdot\dfrac{4}{5}=\dfrac{1}{2}-\dfrac{1}{6}=\dfrac{1}{3}\)
hay \(x=\dfrac{1}{3}\cdot\dfrac{5}{4}=\dfrac{5}{12}\)
b: Ta có: \(\dfrac{1}{4}+\dfrac{1}{2}:x=-3\)
\(\Leftrightarrow\dfrac{1}{2}:x=-3-\dfrac{1}{4}=-\dfrac{13}{4}\)
hay \(x=\dfrac{1}{2}:\dfrac{-13}{4}=\dfrac{1}{2}\cdot\dfrac{-4}{13}=-\dfrac{2}{13}\)

a, Tứ giác ABCM có E là trung điểm AC,BM nên là hình bình hành
Vậy AM=BC
b, Tứ giác ACBN có D là trung điểm AB,CN nên là hình bình hành
\(\Rightarrow\)AN=BC, AN//BC
Mà AM//BC (ABCM là hbh) nên A, M, N thẳng hàng (tiên đề Ơ-clít)
Lại có AN=BC và AM=BC nên AM=AN suy ra đpcm

Bài 3:
a: Xét ΔOCA và ΔOCB có
OC chung
\(\widehat{AOC}=\widehat{BOC}\)
OA=OB
Do đó: ΔOCA=ΔOCB
b: Xét ΔOHA và ΔOHB có
OA=OB
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOHA=ΔOHB
Suy ra: HA=HB
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(1)
Ta có: CB=CA
nên C nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OC là đường trung trực của AB
hay OC\(\perp\)AB
Bài 1:
a: Xét ΔCAB và ΔCDE có
CA=CD
\(\widehat{ACB}=\widehat{DCE}\)
CB=CE
Do đó: ΔCAB=ΔCDE
b: Ta có: ΔCAB=ΔCDE
nên \(\widehat{CAB}=\widehat{CDE}\)
mà \(\widehat{CAB}=80^0\)
nên \(\widehat{CDE}=80^0\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DE

\(a,\)Nếu hai đại lượng y liên hệ với đại lượng x theo công thức \(y=\dfrac{a}{x}\) hay \(xy=a\) (a là một hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
\(b,y=\dfrac{a}{x}\Leftrightarrow xy=a\Leftrightarrow a=-12\cdot\left(-2\right)=24\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{a}{y}\\y=\dfrac{a}{x}\end{matrix}\right.\\ \Rightarrow x=-6;y=-4\\ x=-3;y=-8\\ x=4;y=6\\ x=12;y=2\)

Gọi số học sinh khối 6;7;8;9 lần lượt là a,b,c,d
Ta có: a:b=2:3
nên \(\dfrac{a}{2}=\dfrac{b}{3}\)
hay \(\dfrac{a}{8}=\dfrac{b}{12}\left(1\right)\)
Ta có: b:c=4:5
nên \(\dfrac{b}{4}=\dfrac{c}{5}\)
hay \(\dfrac{b}{12}=\dfrac{c}{15}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(\dfrac{a}{8}=\dfrac{b}{12}=\dfrac{c}{15}\)
hay \(\dfrac{a}{16}=\dfrac{b}{24}=\dfrac{c}{30}\left(3\right)\)
Ta có: c:d=6:7
nên \(\dfrac{c}{6}=\dfrac{d}{7}\)
hay \(\dfrac{c}{30}=\dfrac{d}{35}\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(\dfrac{a}{16}=\dfrac{b}{24}=\dfrac{c}{30}=\dfrac{d}{35}\)
mà a+b+c+d=210
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{16}=\dfrac{b}{24}=\dfrac{c}{30}=\dfrac{d}{35}=\dfrac{a+b+c+d}{16+24+30+35}=\dfrac{210}{105}=2\)
Do đó: a=32; b=48; c=60; d=70

a) ta có |x-3,5|>=0 với mọi x
=> 0,5-|x-3,5|<=0.5
dấu = xảy ra <=> x=3.5
b) ta có 1.4-x>=0 với mọi x
=> -|1.4-x|-2<= -2
dấu = xảy ra <=> x=1.4
\(A=0,5-\left|x-3,5\right|\)
Vì \(\left|x-3,5\right|\)luôn lớn hơn hoặc bằng 0 với mọi x
=>\(-\left|x-3,5\right|\)luôn nhỏ hơn hoặc bằng 0 với mọi x
=>\(0,5-\left|x-3,5\right|\)luôn nhỏ hơn hoặc bằng 0,5 với mọi x
Vậy GTLN của biểu thức A là 0,5
Dấu "=" xảy ra khi \(\left|x-3,5\right|=0\)
=>\(x-3,5=0\)
\(x=3,5\)
Vậy biểu thức A đạt giá trị lớn nhất là 0,5 khi x=3,5
\(B=-\left|1,4-x\right|-2\)
Vì \(\left|1,4-x\right|\)luôn lớn hơn hoặc bằng 0 với mọi x
=>\(-\left|1,4-x\right|\)luôn nhỏ hơn hoặc bằng 0 với mọi x
=>\(-\left|1,4-x\right|-2\)luôn nhỏ hơn hoặc bằng -2 với mọi x
Vậy biểu thức A đạt GTLN là -2
Dấu "=" xảy ra khi \(\left|1,4-x\right|=0\)
=>\(1,4-x=0\)
\(x=1,4\)
Vậy biểu thức A đạt giá trị lơn nhất là -2 khi x=1,4

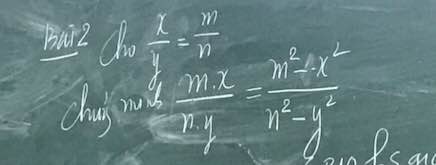
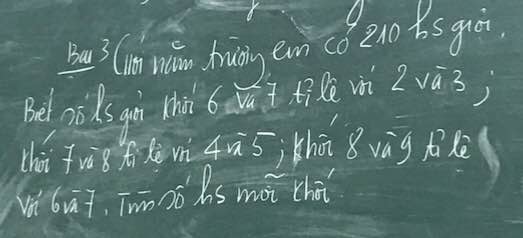





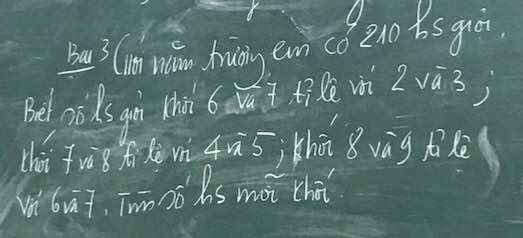
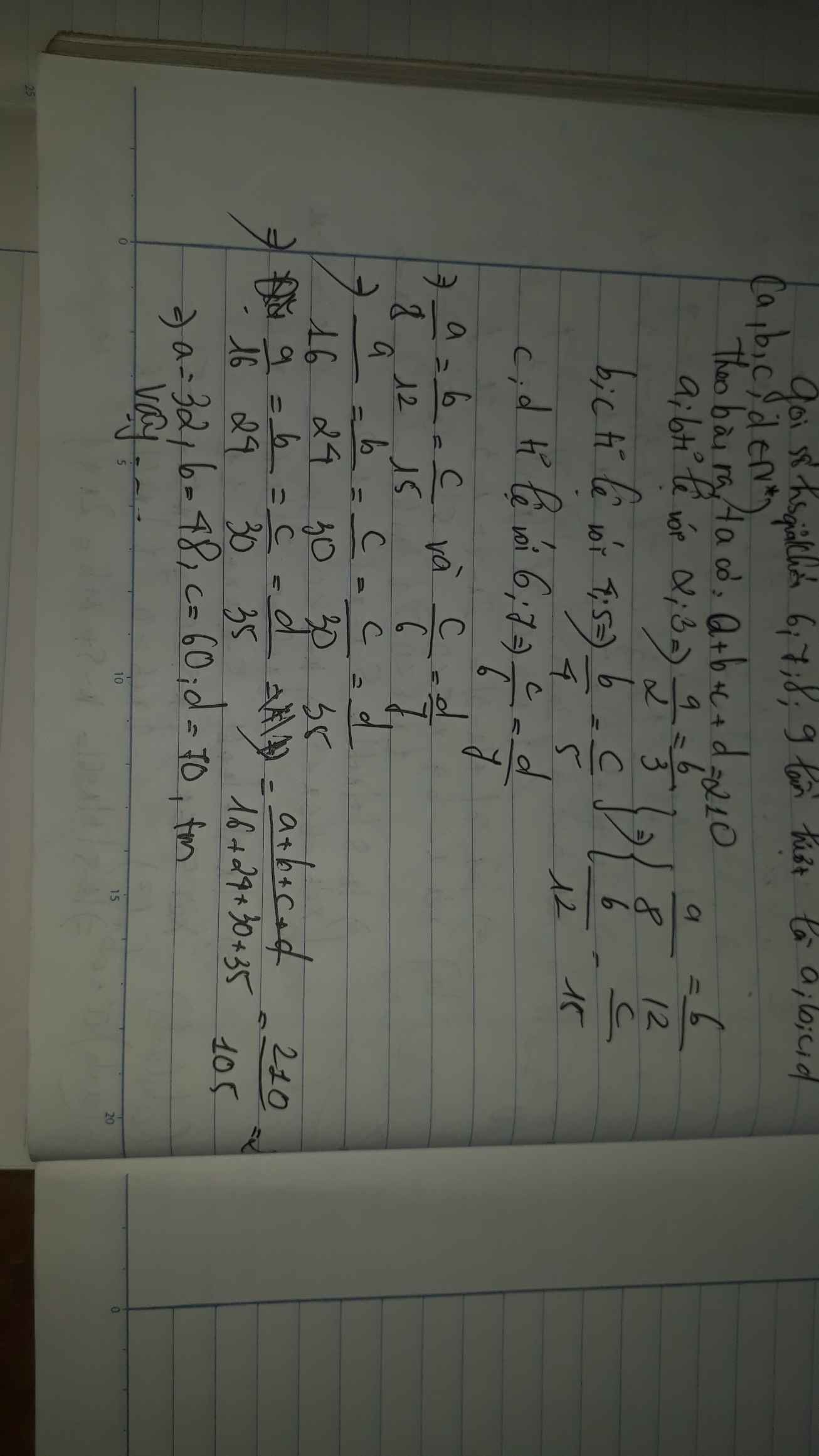
\(x^2+1=\dfrac{25}{16}\)
\(x^2=\dfrac{25}{16}-1\)
\(x^2=\dfrac{9}{16}\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=\dfrac{3}{4}\end{matrix}\right.\)
Vậy...