Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Giả sử z = a + b i
với a , b ∈ ℝ ⇒ M a , b , M ' a , − b .
Ta có:
z 4 + 3 i = a + b i 4 + 3 i = 4 a − 3 b + i 4 b + 3 a ⇒ N 4 a − 3 b ; 4 b + 3 a , N ' 4 a − 3 b ; − 4 b − 3 a
Để M, M’, N, N’ là 4 đỉnh của hình chữ nhật thì M phải có cùng tọa độ với N và N’
⇔ b = ± 4 b + 3 a ⇔ b = − a b = − 3 a 5 ⇒ M nằm trên đường thẳng Δ 1 : x + y = 0 hoặc Δ 2 : 3 x + 5 y = 0
Xét điểm I 5 ; − 4 ⇒ z + 5 i − 5 = M I = M i n d I , Δ 1 , d I , Δ 1 = 1 2 .

Đáp án D.
Ta có y ' = 6 x 2 + 6 1 - m x + 6 m - 2 .
Hàm số có điểm cực trị x 0 = 2 ⇒ 6 . 2 2 + 6 . 1 - m . 2 + 6 . m - 2 = 0 ⇔ m = 4 .
Với m = 4 hàm số có thêm một điểm cực trị x 1 = m - 2 2 = 1 .
Hàm số đã cho trở thành y = 2 x 3 - 9 x 2 + 12 x + n .
Hàm số này có hai cực trị là y 0 = y 2 = n + 4 và y 1 = y 1 = n + 5 .
Hàm số có hai cực trị đều dương ⇔ n + 4 > 0 n + 5 > 0 ⇔ n > - 4
Vậy giá trị nguyên nhỏ nhất của n là ‒3. Do đó giá trị nhỏ nhất của m + n (với m , n nguyên) là 4 + - 3 = 1 . Chọn đáp án D.

Đáp án C
Ta có y = - 1 + 2 - 3 . 2 sin x c o s x + 2 cos 2 x = 2 - 3 . sin 2 x + cos 2 x .
Áp dụng bất đẳng thức Bunhicopxki, có
2 - 3 . sin 2 x + cos 2 x 2 ≤ 2 - 3 2 + 1 2 . sin 2 2 x + cos 2 2 x = 8 - 4 3
Suy ra y 2 ≤ 8 - 4 3 ⇔ 8 - 4 3 ≤ y ≤ 8 - 4 3 . Vậy M + N + 2 = 2.

Đáp án C
Ta có: y = − 1 + 2 − 3 .2 sin x cos x + 2 cos 2 x
= 2 − 3 . sin 2 x + cos 2 x
Áp dụng bất đẳng thức Bunhiacopxki, có:
2 − 3 . sin 2 x + cos 2 x 2 ≤ 2 − 3 2 + 1 2 . sin 2 2 x + cos 2 2 x = 8 − 4 3
Suy ra y 2 ≤ 8 − 4 3 ⇔ − 8 − 4 3 ≤ y ≤ 8 − 4 3 .
Vậy M + N + 2 = 2

Đáp án D
ĐK xác định của hàm số là − 4 ≤ x ≤ 4
y ' = 1 − x 16 − x 2 = 16 − x 2 − x 16 − x 2 ⇒ y ' = 0 ⇔ x = 2 2
Các giá trị tại biên và điểm cực trị là
y − 4 = − 4 y 4 = 4 y 2 2 = 4 2 ⇒ M . N = 4 2 . − 4 = − 16 2

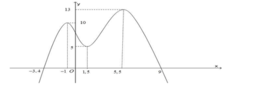
Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
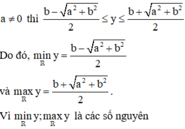
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
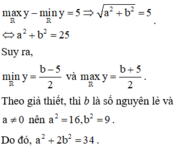
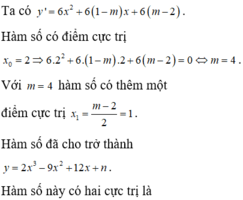


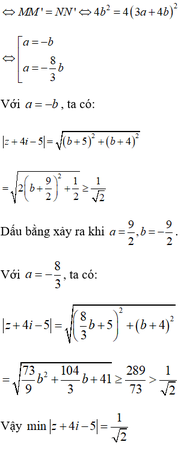
n=972