Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài AB là x
Thời gian dự kiến là x/40
Theo đề, ta có: 3/10+(x-18)/50+2/5=x/40
=>7/10+1/50x-9/25-1/40x=0
=>x*(-1/200)=-17/50
=>x=68


Vì thời gian thực tế đi chậm hơn thời gian dự định là 18 phút nên ta có phương trình:
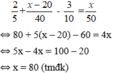
Vậy chiều dài quãng đường AB là 80km.

Gọi vận tốc dự định là xx(km/h)
Khi đó, thời gian dự định là 260/x (h)
Thời gian thực tế là 120/x+140/x+10 (h)
Do xe đến B sớm hơn dự định 20′ =1/3(h) nên ta có
120/x+140/x+10= 260/x− 1/3
<−>140/x+10=140/x−1/3
<−>140/x=140(x+10)−1/3 x (x+10)
<−>0=4200−x(x+10)
<−>x^2+10x−4200=0
<−>(x−60)(x+70)=0
Vậy x=60 hoặc x=−70 (loại)
Vậy vận tốc dự định của ô tô là 60(km/h).

Gọi quãng đường AB= s
thời gian xe con đi hết quãng đường AB t1= s/v1 +2/3 = s/60+2/3
thời gian xe tải đi hết quãng đường AB t2= s/(2v2) +s/2(v2+10) = s/80 +s/100
t2= t1+1/2 ---> s/80+ s/100 = s/60 +2/3 +1/2.
Giải phương trình trên ta được s= 200 km
Một tàu thủy chạy trên khúc sông dài 80km, cả đi cả về mất 8 giờ 20 phút. Tính vận tốc của tàu khi nước yên lặng, biết rằng vận tốc của dòng nước là 4 km/h.

Bài 1:
Đổi 50 phút thành $\frac{5}{6}$ giờ.
Thời gian xe tải đi từ A đến B: $t_1=\frac{AB}{v_{tải}}=\frac{AB}{40}$ (h)
Thời gian xe con đi từ A đến B: $t_2=2+\frac{AB-2.50}{50+10}=2+\frac{AB-100}{60}$ (h)
$t_1-t_2=\frac{AB}{40}-(2+\frac{AB-100}{60})$
$\Leftrightarrow \frac{5}{6}=\frac{AB}{40}-2-\frac{AB-100}{60}$
$\Rightarrow AB= 140$ (km)
Bài 2:
Đổi 5 giờ 30 phút thành $5,5$ giờ.
Thời gian đi từ A-B là: $\frac{AB}{30}$ (h)
Thời gian làm việc: $1$ (h)
Thời gian đi từ B-A là: $\frac{AB}{24}$ (h)
Tổng thời gian hao phí:
$\frac{AB}{30}+1+\frac{AB}{24}=5,5$
$\Rightarrow AB=60$ (km)

Gọi vận tốc dực định là x (km/giờ)
Thời gian định đi là: 120/x (giờ)
Thời gian đi 1/3 quãng đường đầu là: 40/x (giờ)
Vận tốc quãng đường còn lại là: x + 10 (km/giờ)
Thời gian còn lại là: 80/x + 10 (giờ)
Theo đề bài, ta có:
\(\frac{40}{x}+\frac{80}{x+10}-\frac{120}{x}=-\frac{24}{60}\)
\(\Leftrightarrow\orbr{\begin{cases}x=40\\x=-50\end{cases}}\)
Vận tốc dự định của người đó là 40 (km/giờ)
Thời gian lăn bánh là:
\(\frac{40}{40}+\frac{80}{50}=2,6\)(giờ)

Đổi \(30phút=\dfrac{1}{2}\left(h\right)\)
Gọi vận tốc dự định của xe máy là x (km/h; x > 0 )
Thì vận tốc đi nửa quãng đường còn lại là \(x+10\)
Nửa quãng đường là : \(\dfrac{1}{2}.120=60\left(km\right)\)
Thời gian xe dự định đi từ A đến B là \(\dfrac{120}{x}\left(h\right)\)
Thời gian xe đi được nửa quãng đường đầu là \(\dfrac{60}{x}\left(h\right)\)
Thời gian xe đi nửa quãng đường còn lại khi tăng thêm 10km/h là \(\dfrac{60}{x+10}\)
Vì tăng thêm 10km/h ở nửa sau quãng đường nên xe đến B sớm hơn \(\dfrac{1}{2}\left(h\right)\) so với dự định nên ta có phương trình.
\(\dfrac{60}{x}+\dfrac{60}{x+10}+\dfrac{1}{2}=\dfrac{120}{x}\)
\(\Leftrightarrow120\left(x+10\right)+120x+x\left(x+10\right)=240\left(x+10\right)\)
\(120x+1200+120x+x^2+10x=240x+2400\)
\(\Leftrightarrow x^2+120x+120x+10x-240x+1200-2400=0\)
\(\Leftrightarrow x^2+10x-1200=0\)
\(\Leftrightarrow x^2-30x+40x-1200=0\)
\(\Leftrightarrow x\left(x-30\right)+40\left(x-30\right)=0\)
\(\Leftrightarrow\left(x+40\right)\left(x-30\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+40=0\\x-30=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-40\left(loại\right)\\x=30\left(nhận\right)\end{matrix}\right.\)
Vậy vận tốc dự định của xe máy là 30km/h
Gọi vận tốc dự định của xe máy là x ( km/h x > 0 )
Thời gian xe máy dự định đi từ A đến B = 120/x ( giờ )
Vận tốc xe đi nửa quãng đường sau = x + 10 (km/h)
Thời gian xe máy đi nửa quãng đường đầu = 60/x ( giờ )
Thời gian xe máy đi nửa quãng đường sau = 60/(x+10) giờ )
Theo bài ra ta có phương trình : 60x+60x+10=120x−1260x+60x+10=120x−12
Giải phương trình thu được x = -40 ( loại ) ; x = 30 ( tm )
Vậy vận tốc dự định của xe máy là 30km/h

Gọi quãng đường AB là x(x>0)
Thời gian đi là \(\dfrac{x}{45}\)
Thời gian về là \(\dfrac{x}{50}\)
10 phút = \(\dfrac{1}{6}\) giờ
Theo đề bài ta có pt:
\(\dfrac{x}{45}-\dfrac{x}{50}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{10x-9x}{450}=\dfrac{75}{450}\)
\(\Leftrightarrow x=75\left(km\right)\left(tm\right)\)
Vậy quãng đường AB dài 75km
Gọi độ dài đoạn đường AB là \(x\left(x>0\right)\)
\(\Rightarrow\) Thời gian dự định là \(\dfrac{x}{40}\) giờ
Xe đi trong \(18\) phút \(=\dfrac{3}{10}\) giờ thì đoạn đường đã đi được là:
\(40\times\dfrac{3}{10}=12km\)
\(\Rightarrow\) Đoạn đường còn lại là \(x-12\) km
Thời gian đi đoạn đường còn lại là:
\(\dfrac{x-12}{40+10}=\dfrac{x-12}{50}\) giờ
Tổng thời gian thực tế đi là:
\(\dfrac{3}{10}+\dfrac{x-12}{50}\) giờ
Do đến sớm hơn \(24\) phút \(=\dfrac{2}{5}\) giờ nên ta có phương trình sau:
\(\dfrac{x}{40}-\left(\dfrac{3}{10}+\dfrac{x-12}{50}\right)=\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{x}{40}-\dfrac{3}{10}-\dfrac{x}{50}+\dfrac{12}{50}=\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{x}{40}-\dfrac{x}{50}=\dfrac{2}{5}+\dfrac{3}{10}-\dfrac{12}{50}\)
\(\Leftrightarrow\dfrac{x}{90}=\dfrac{23}{50}\)
\(\Leftrightarrow x=\dfrac{23}{50}\times90=\dfrac{207}{5}km\)