Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C

+ Độ giảm biên độ trong nửa chu kì: ![]()
+ Theo yêu cầu của đề: 0,04 + (0,04 – ΔA) < S < 0,04 + 2(0,04 – ΔA)
=> 0,08 – 0,4μ < S < 0,12 – 0,8μ
+ Tới khi dừng hẳn: ![]()
+ 0,08 – 0,4μ < 4.10-3 /μ => (μ – 0,1)2 > 0
+ 4.10-3 /μ < 0,12 – 0,8μ => μ2 – 0,15μ + 0,005 < 0 => 0,05 < μ < 0,1.

Đáp án D
Phương pháp: Sử dụng lí thuyết về bài toán dao động tắt dần của con lắc lò xo
Cách giải:
Khi vật dừng lại, toàn bộ cơ năng chuyển thành công của lực ma sát:
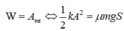
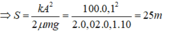

Đáp án C.
Lời giải chi tiết:
Theo giả thiết
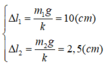
=> Tại vị trí cân bằng của hai vật lò xo dãn 12,5 cm
Thả vật tại vị trí lò xo dãn 20cm =>A=7,5cm
Khi về tới O thì lò xo dãn 10cm =>x = -2,5cm
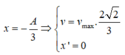
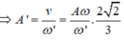
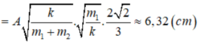

Hướng dẫn:
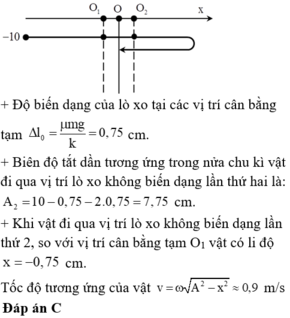
Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 2.40.10 − 3 .10 20 = 4 m m
→ Biên độ dao động của lò xo trong nửa chu kì đầu A 1 = X 0 – x 0 = 6 – 0 , 4 = 5 , 6 c m .
+ Lò xo bị nén lớn nhất khi vật đi đến biên âm ứng với nửa chu kì đầu.
→ Độ nén của lò xo khi đó là Δ l m a x = A 1 + x 0 = 5 , 6 – 0 , 4 = 5 , 2 c m .
Đáp án A

Chọn A
+ Tần số góc của con lắc: 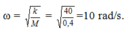
+ Tốc độ của M khi đi qua VTCB: v = ωA = 50cm/s.
+ Tốc độ của (M + m) khi qua VTCB: 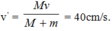
+ Tần số góc của hệ con lắc: 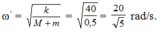
+ Biên độ dao động của hệ: ![]()

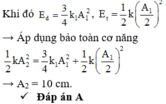
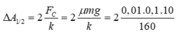
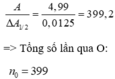
a)Biên độ: \(A=20cm=0,2m\)
Tần số góc: \(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{400}{0,1}}=20\sqrt{10}=20\pi\)
Chu kì: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{20\pi}=\dfrac{1}{10}=0,1s\)
Tần số dao động: \(f=\dfrac{1}{T}=\dfrac{1}{0,1}=10Hz\)
b)Tại vị trí \(A=20cm\):
\(W_đ=0J\)
\(W_{tmax}=W_c=\dfrac{1}{2}kx^2=\dfrac{1}{2}m\omega^2x^2=\dfrac{1}{2}\cdot0,1\cdot\left(20\pi\right)^2\cdot0,2^2=8J\)
c)Thời điểm lần thứ 2024 lò xo:
\(t_{2024}=2022+2=1011T+t'\)
\(t'=\dfrac{240}{360}T=\dfrac{2}{3}T=\dfrac{1}{15}s\)
\(t_{2024}=1011\cdot\dfrac{1}{10}+\dfrac{1}{15}=\dfrac{607}{6}s\approx101,17s\)
Tại sao A=20cm vậy ạ với lại cho em cách làm câu c với ạ