Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi vận tốc của người đó khi đi là x km/h(x > 6)
Vận tốc khi về là x – 6 (km/h)
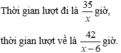
Vì thời gian lượt về bằng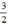 
thời gian lượt đi nên ta có phương trình:
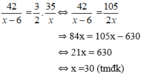
Vậy vận tốc lượt đi của người đó là 30km/h, vân tốc lượt về là 24km/h
`Answer:`
Đặt vận tốc của xe gắn máy lúc đi là `x`
Vậy vận tốc của xe gắn máy lúc về là `x-6`
Thời gian đi là `\frac{35}{x}` giờ
Thời gian về là `\frac{42}{x-6}` giờ
Ta có `2/3.\frac{42}{x-6}=\frac{35}{x}`
`<=>\frac{84}{3x-18}=\frac{35}{x}`
`<=>84x-105x=-630`
`<=>-21x=-630`
`<=>x=30` \(km/h\)
Vậy vận tốc lúc quay về là: `x-6=30-6=24` \(km/h\)
Đổi 3/2 = 1,5 ( giờ )
Gọi vận tốc lúc đi là x ( x > 0 )
Vân tốc lúc về là x - 6
Thời gian đi là \(\frac{35}{x}\)
Thời gian về là \(\frac{42}{x-6}\)
Theo đề bài ta có phương trình:
\(\frac{42}{x-6}-1,5.\frac{35}{x}\)
Giải phương trình ta được vân tốc đi là 30km/h
vân tốc về là 24km/h
Gọi \(x\left(km/h\right)\) là vận tốc lúc đi \(\left(x>0\right)\)
Vận tốc lúc về là: \(x+3\left(km/h\right)\)
Thời gian đi là: \(\dfrac{33}{x}\left(h\right)\)
Thời gian về là: \(\dfrac{62}{x+3}\left(h\right)\)
Đổi: 1 giờ 30 phút = 1,5 giờ
Do thời gian đi nhiều hơn thời gian về 1 giờ 30 phút nên ta có:
\(\dfrac{33}{x}-\dfrac{62}{x+3}=1,5\)
\(\Leftrightarrow\dfrac{33\left(x+3\right)}{x\left(x+3\right)}-\dfrac{62x}{x\left(x+3\right)}=1,5\)
\(\Leftrightarrow\dfrac{33x+99-62x}{x\left(x+3\right)}=1,5\)
\(\Leftrightarrow\dfrac{99-29x}{x\left(x+3\right)}=1,5\)
\(\Leftrightarrow\dfrac{99-29x}{x\left(x+3\right)}=\dfrac{3}{2}\)
\(\Leftrightarrow3x^2+9x=198-58x\)
\(\Leftrightarrow3x^2+67x-198=0\)
\(\Leftrightarrow x\approx3\left(km/h\right)\left(tm\right)\)
Gọi vận tốc lúc đi là x
=>vận tốc lúc về là x+3
Theo đề, ta có: \(\dfrac{33}{x}-\dfrac{62}{x+3}=\dfrac{3}{2}\)
=>\(\dfrac{33x+99-62x}{x\left(x+3\right)}=\dfrac{3}{2}\)
=>3(x^2+3x)=2(-29x+99)
=>3x^2+6x+58x-198=0
=>3x^2+64x-198=0
=>\(\left[{}\begin{matrix}x\simeq2,74\left(nhận\right)\\x\simeq-24,07\left(loại\right)\end{matrix}\right.\)