Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Do lực cản sinh công làm biến đổi động năng của vật nên áp dụng định lí biến thiên động năng:
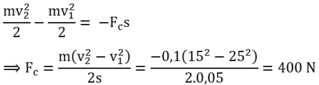

Lời giải
Do lực cản sinh công làm biến đổi động năng của vật nên áp dụng định lí biến thiên động năng:
m v 2 2 2 − m v 1 2 2 = − F c s = > F c = − m v 2 2 − v 1 2 2 s = − 0 , 1 15 2 − 25 2 2.0 , 05 = − 400 N
Đáp án: D

Chọn D.
Do lực cản sinh công làm biến đổi động năng của vật nên áp dụng định lí biến thiên động năng:
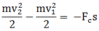
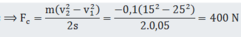

Chọn B.
Áp dụng định luật bảo toàn động lượng cho hệ (xe + đanh) ngay khi va chạm:


Chọn B.
Áp dụng định luật bảo toàn động lượng cho hệ (xe + đanh) ngay khi va chạm:
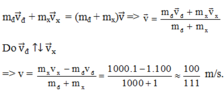
Động năng của hệ ngay trước va chạm là:
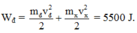
Động năng của hệ sau va chạm là:
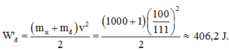
Theo định luật bảo toàn năng lượng Q = Wđ – W’đ = 5500 – 406,2 ≈ 5093,8 J.

Chọn B.
Hệ viên đạn (hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
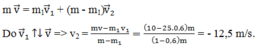
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.

Lời giải
Ta có:
+ Hệ viên đạn ( hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
+ Gọi m 1 = 0 , 6 m là khối lượng của mảnh thứ nhất
=> Khối lượng của mảnh còn lại là m 2 = m − m 1 = m − 0 , 6 m = 0 , 4 m
+ Áp dụng định luật bảo toàn động lượng ta có: p → = p → 1 + p → 2
m v → = m 1 v → 1 + m − m 1 v → 2
Theo đầu bài, ta có mảnh 1 tiếp tục bay theo hướng cũ
=> v → 1 ↑ ↑ v →
Ta suy ra:
v 2 = m v − m 1 v 1 m − m 1 = ( 10 − 25.0 , 6 ) m ( 1 − 0 , 6 ) m = − 12 , 5 m / s
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.
Đáp án: B

Chọn B.
Hệ viên đạn (hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
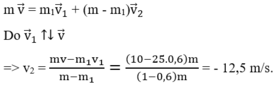
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.

Chọn C.
Ta có: v 2 = 36 km/h = 10 m/s.
Va chạm giữa viên đạn và toa xe là va chạm mềm nên động lượng của hệ (đạn + xe) là không đổi:
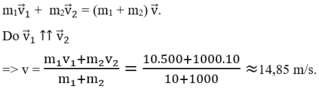
Ta có: \(v^2-v_0^2=2aS\Rightarrow v=\sqrt{2.24000.0,7}=40\sqrt{21}\left(m/s\right)\)
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.0,03.\left(40\sqrt{21}\right)^2=504\left(J\right)\)