Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tốc độ góc và gia tốc hướng tâm của vệ tinh được tính theo các công thức
ω = 2 π /T = (2.3.14)/(88.60) ≈ 1.19. 10 - 3 (rad/s)
a h t = ω 2 (R + h) = 1 . 19 . 10 - 3 2 .6650. 10 3 = 9,42 m/ s 2

Ta có:
+ Tốc độ góc: ω = 2 π T
+ Lực hướng tâm: F h t = m v 2 r = m ω 2 r
=> Ta suy ra:
Độ lớn lực hướng tâm tác dụng lên vệ tinh:
F h t = m ω 2 r = m 4 π 2 ( R + h ) T 2 = 100.4. π 2 .6553.1000 ( 5.10 3 ) 2 ≈ 1035 N
Đáp án: C

a.
Ta có:
\(v=\sqrt{\dfrac{g_0\cdot R^2}{R+h}}=\sqrt{\dfrac{9,8+\left(6400\cdot1000\right)^2}{6400\cdot1000+25630\cdot1000}}=3540,1\left(\dfrac{m}{s}\right)\)
Tốc độ góc:
\(\omega=\dfrac{v}{R}=\dfrac{3540,1}{6400\cdot1000}=5,5\cdot10^{-4}\left(\dfrac{rad}{s}\right)\)
b.
\(a_{ht}=\dfrac{v^2}{R}=\dfrac{3540,1^2}{6400\cdot1000}\approx2\left(\dfrac{m}{s^2}\right)\)
Không có tốc độ hướng tâm, chỉ có gia tốc hướng tâm bạn nhé

Lực hấp dẫn đóng vai trò là lực hướng tâm.
\(F_{hd}=F_{ht}\)\(\Rightarrow G\cdot\dfrac{M\cdot m}{\left(R+R\right)^2}=\dfrac{mv^2}{R}\)
\(\Rightarrow v=\sqrt{\dfrac{G\cdot M}{2R}}\)
Mà gia tốc tại mặt đất:
\(g=\dfrac{GM}{R^2}=9,8\)m/s2\(\Rightarrow\dfrac{1}{4}mg=\dfrac{mv^2}{2R}\Rightarrow v=\sqrt{\dfrac{R\cdot g}{2}}=\sqrt{\dfrac{6400\cdot1000\cdot9,8}{2}}=5600\)m/s
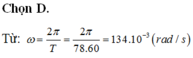
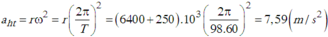

Chọn D.