Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quãng đường vật đi trong giây cuối cùng là 63,7m.
\(\Rightarrow\) Thời gian rơi của vật trên cae quãng đường:
\(S=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-1\right)^2\)
\(\Rightarrow\dfrac{1}{2}\cdot9,8\cdot t^2-\dfrac{1}{2}\cdot9,8\cdot\left(t-1\right)^2=63,7\Rightarrow t=7\left(s\right)\)
Độ cao S để thả vật rơi: \(S=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot9,8\cdot7^2=240,1\left(m\right)\)
Vận tốc vật lúc chạm đất: \(v=g\cdot t=9,8\cdot7=68,6\)(m/s)

Nếu gọi s là quãng đường viên đá đi được sau khoảng thời gian t kể từ khi bắt đầu rơi tới khi chạm đất và gọi s 1 là quãng đường viên đá đi được trước khi chạm đất 1 s, tức là sau khoảng thời gian t 1 = t -1 thì ta có các công thức
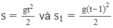
Từ đó suy ra quãng đường viên đá đi được trong 1 s cuối trước khi chạm đất là:
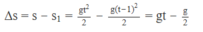
Với ∆ s = 24,5 m và g = 10 m/ s 2 , ta tìm được khoảng thời gian rơi tự do của viên đá
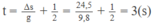

Chọn chiều dương hướng xuống. Gọi t là thời gian vật rơi đến đất.
Quãng đường vật rơi trong t và t - 1 giây đầu tiên:
h = 1 2 g t 2 = 5 t 2 ; h ' = 1 2 g ( t − 1 ) 2 = 5 t − 1 2 .
Ta có h − h ' = 15 m hay 5 t 2 − t t − 1 2 = 15 ⇒ t = 2 s
Độ cao nơi thả vật: h = 5 t 2 = 5.2 2 = 20 m

a) Thời gian vật rơi chạm đất là:
\(S=\dfrac{1}{2}gt^2\Rightarrow t=\sqrt{\dfrac{2S}{g}}=\sqrt{\dfrac{2.70}{9,8}}\approx3,78\left(s\right)\)
b) Quãng được vật rơi trong giây thứ ba là:
\(S=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-1\right)^2=\dfrac{1}{2}.9,8.3^2-\dfrac{1}{2}.9,8.\left(3-1\right)^2=24,5\left(m\right)\)

Chọn C.
Độ cao của vật: H = 5.82 = 320 m
Thời gian vật rơi 10 m cuối cùng:
10 = 320 – 0,5.10(8 – Δt)2 → Δt = 0,126 s.
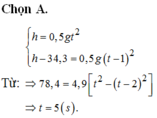
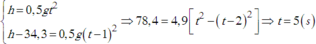
Thời gian vật đó chạm đất là:
\(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2.34,3}{9,8}}=2,65\) (s)