Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kì dao động của vật T = 2π/ω = 0,5s
Xét thời gian 7/48s = 7T/14 = T/8 + T/6
Ta có hình vẽ
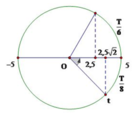
Từ hình vẽ ta thấy rằng, sau 7/48s vật đi qua vị trí có li độ x = 2,5 cm
Đáp án D

Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
Ta có: \(x=2,5\sqrt{2}=\dfrac{A\sqrt{2}}{2}\) và đang có xu hướng giảm.
Lúc này vật ở thời điểm: \(t_1=\dfrac{T}{8}\)
Tại thời điểm: \(t=\dfrac{7}{48}s=\dfrac{7T}{14}=\dfrac{T}{8}+\dfrac{T}{6}\)
Dựa vào vòng tròn lượng giác \(\Rightarrow x=2,5cm\)

Ta có:
- Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
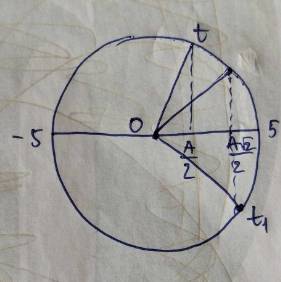
\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)
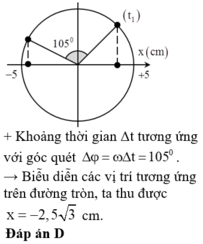
Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)
+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)
\(x_1=A.sin\left(15^o\right)=2,59cm\)
+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)
\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)

Gọi phương trình dao động \(x=A\cos\left(\omega t+\varphi\right).\left(1\right)\)
Chu kỳ T là thời gian thực hiện 1 dao động toàn phần.
=> \(T=\frac{\Delta t}{N}=\frac{100}{50}=2s.\)
=> \(\omega=\frac{2\pi}{T}=\pi.\)(rad/s)
Áp dụng công thưc mối quan hệ giữa li độ tức thời x, biên độ A và vận tốc tại vị trí li độ đó v là
\(A^2=x^2+\frac{v^2}{\omega^2}=20^2+\frac{\left(4\pi\sqrt{3}\right)^2}{\pi^2}=448\Rightarrow A=21,166cm.\)
Mình nghĩ bài của bạn số hơi xấu?:))))
Li độ tại thời điểm \(\left(t+\frac{1}{3}\right)s\) là
Bạn có 2 cách để làm thay t ở công thức (1) bằng t+1/3s.
Tuy nhiên mình hay dùng cách 2 đường tròn như sau
Thời điểm t vật có li độ 20 cm thêm 1/3 s nữa thì góc quay được là \(\varphi=\frac{1}{3}.\pi.\)
A 0 20 A 19 N M 10
Bài của bạn số xấu quá nên tìm góc cũng xấu.:))))))
\(\cos10^0=\frac{x}{A}\Rightarrow x=A\cos10^0\approx20,84cm.\)

Chọn đáp án D
ω = 2 π ⇒ T = 1 ( s ) ⇒ 0 , 125 ( s ) = 1 8 T ⇒ △ φ = π 4 .
x 0 = 5 c m ⇒ cos φ 0 = 5 20 ⇒ φ 0 = − 1 , 318 ⇒ φ 1 = φ 0 + Δ φ = − 0 , 533
⇒ x 1 = A . cos φ 1 = 17 , 2 c m .


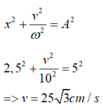
Chu kì \(T=\dfrac{2\pi}{\omega}=0,5s\)
Trong thời gian 7/48s thì véc tơ quay đã quay một góc là:
\(\alpha=\dfrac{\dfrac{7}{48}}{0,5}.360=26,25^0\)
Biểu diễn dao động bằng véc tơ quay, ban đầu qua li độ \(2,5\sqrt 2\) và đang giảm
ứng với vị trí M như hình vẽ
M N
Lúc sau, véc tơ quay đến N, hình chiếu của N lên trục tọa độ sẽ cho biết li độ mới.
\(x=5.\cos(45-26,25)\approx4,73cm\)
@Thư Hoàngg: Bạn Quang Hưng nhầm trong việc tính góc α,
giá trị đúng phải là: \(\alpha = 105^0\), như vậy ban đầu véc tơ quay ở M quay 1050
sẽ đến N, khi đó ON tạo với Ox 1 góc là: 105 - 45 = 600
Suy ra: \(x=5.\cos(60^0)=2,5cm.\)