

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




+ Chu kì dao động của vật là:
![]()
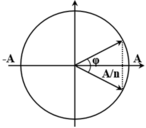
+ Trong một chu kì, khoảng thời gian mà
![]()
là ∆ t được biểu diễn như hình.
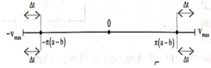
+ Theo đề ta có:
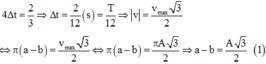
+ Theo (1) suy ra a>b kết hợp với giả thiết ffề bài suy ra thời gian ngắn nhất giữa hai lần liên tiếp vật cách vị trí cân bằng một khoảng bằng a và b được biểu diễn như hình vẽ.
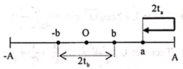
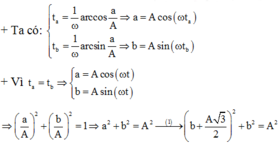
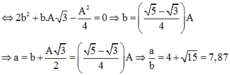
=> Chọn D.

Đáp án D
Chu kì dao động của vật là T = 2 π ω
Khoảng thời gian trong một chu kì tốc độ không vượt quá là: 2 π n - m cm / s
![]()
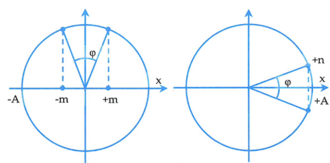
Từ hình vẽ ta có:
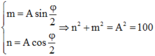
Kết hợp hai phương trình trên ta có:
![]()

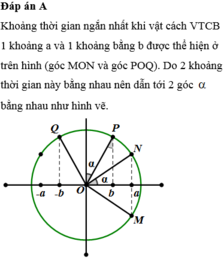
C ó sin α = b A cos α = a A ⇒ sin 2 α + cos 2 α = 1 ⇔ b 2 A 2 + a 2 A 2 = 1 ⇔ a 2 + b 2 = 100

Đáp án A
Từ đáp án của bài ra suy ra a và b khác nhau.
Từ giả thiết: Khoảng thời gian ngắn nhất giữa hai lần liên tiếp vật cách vị trí cân bằng một khoảng bằng a với khoảng thời gian ngắn nhất giữa hai lần liên tiếp vật cách vị trí cân bằng một khoảng bằng b ta có phương trình: (Lấy trường hợp đại diện)
2 ω arcsin a A = 2 ω arccos b A ⇒ a 2 + b 2 = A 2 = 100 1
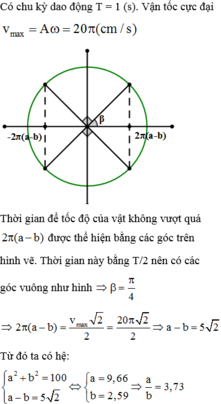
Mặt khác vị trí mà vật có tốc độ 2 π b − a thỏa mãn
x = ± A 2 − v 2 ω 2 = ± a 2 + b 2 − b − a 2 = ± 2 a b
Khi đó khoảng thời gian mà tốc độ của vật không vượt quá 2 π b − a trong một chu kỳ là t = 4 ω arccos 2 a b 10 = 0,5 ⇔ a b = 25 2
Từ (1) và (2) ta có phương trình a 2 + b 2 = 4 a b ⇔ b a = 2 + 3 b a = 2 − 3
Từ đó ta có b a = 2 + 3 ≈ 3,73

Đáp án B
Giả sử x = A cos ω t + φ
Thời gian giữa hai lần liên tiếp vật qua vị trí cân bằng là nửa chu kỳ nên T = 2.0 , 5 = 1 s ⇒ ω = 2 π r a d / s
Quãng đường đi được trong 2s (2 chu kì) là: S = 2.4 A = 32 ⇒ A = 4 c m
Tại thời điểm t = 1 , 5 s vật qua vị trí có li độ x = 2 3 c m theo chiều dương
⇒ 2 3 = 4 cos 3 π + φ − 2 π .4 sin 3 π + φ > 0 ⇒ cos φ = − 3 2 sin φ > 0
Suy ra, có thể lấy φ = − 7 π 6