

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải
Chọn chiều dương trùng chiều chuyển động của vật, ta có vật rơi tự do không vận tốc đầu
=> Phương trình vận tốc của vật:


Biểu thức tổng quát: \(W_đ=\dfrac{1}{2}mv^2\Rightarrow v=\sqrt{\dfrac{2W_đ}{m}}\)
Với Wđ=5 (J) ta có: v=10(m/s)
\(v=v_0+gt\Rightarrow t=\dfrac{v}{g}=\dfrac{10}{10}=1\left(s\right)\)
Với Wđ=20J ta có: v=20(m/s)
\(v=v_0+gt\Rightarrow t=\dfrac{v}{g}=\dfrac{20}{10}=2\left(s\right)\)

m=100g =0,1kg
g =10m/s2
a) Wđ = 20J; t =?
b) s =?; Wđ =4J
GIẢI :
Chọn chiều dương trùng chiều chuyển động của vật, ta có vật rơi tự do không vận tốc đầu
=> Phương trình vận tốc của vật : \(v=v_0+gt=0+gt=10t\)
a) \(W_đ=\frac{1}{2}mv^2=20\left(J\right)\)
<=> \(v=\sqrt{\frac{2W_đ}{m}}=\sqrt{\frac{2.20}{0,1}}=20\left(m/s\right)\)
thời gian kể từ lúc vật bắt đầu rơi đến khi có động năng 20J là : \(t=\frac{v}{10}=\frac{20}{10}=2\left(s\right)\)
b) \(v=\sqrt{\frac{2W_đ}{m}}=\sqrt{\frac{2.4}{0,1}}=4\sqrt{5}\left(m/s\right)\)
Quãng đường vật rơi là :
\(v^2=2gs\Rightarrow s=\frac{v^2}{2g}=\frac{\left(4\sqrt{5}\right)^2}{2.10}=4\left(m\right)\)
Đổi \(100g=0,1kg\)
a) \(W_đ=\frac{1}{2}.mv^2=20\left(J\right)\)
\(\rightarrow20=\frac{1}{2}.0,1v^2\)
\(\rightarrow v=20\left(m/s\right)\)
\(\rightarrow v^2-0=2.g.s\rightarrow20^2-0=2.10.s\rightarrow s=20\left(m\right)\)
b) \(W_đ=\frac{1}{2}.mv^2=20\left(J\right)\)
\(\rightarrow4=\frac{1}{2}.0,1v^2\)
\(\rightarrow v=\sqrt{80}=8,9\left(m/s\right)\)
\(\rightarrow v^2-0=2.g.s\rightarrow8,9^2-0=2.10.s\rightarrow s=3,96\left(m\right)\)
Vậy ...

Chọn gốc tính thế năng (Zn = 0) tại O tức là vị trí vật bắt đầu rơi.
Quãng đường vật rơi được sau 4 giây bằng
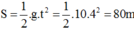
Giá trị đại số của tọa độ Z của vật so với mốc bằng
![]()
Thế năng của vật sau khi rơi được sau 4 giây bằng
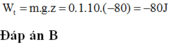

bài 4
giải
vận tốc cực đại trong quá trình rơi đạt được là lúc vật chạm đất (z=0)
ta có \(m.g.h=0,5.mv^2\Rightarrow v=\sqrt{2gh}\)
\(\Rightarrow v=\sqrt{2.10.20}=20m/s\)
bài 3
giải
ta có: m.g.h=2Wđ=1.0,5.m.\(v^2\Rightarrow v=\sqrt{g.h}\)
\(\Rightarrow v=\sqrt{10.20}=10\sqrt{2}m/s\)

1.
Có: \(h=\frac{1}{2}gt^2\)
\(\Rightarrow h=1,25\) m
Vận tốc của vật sau khi ném 0,5s
\(\frac{v-v_0}{\Delta t}=g\) (Vì vật ném lên có nên vật chuyển động chậm dần đều)
\(\Leftrightarrow v=5\) m/s
Thế năng của vật sau khi ném 0,5s:
\(W=W_đ+W_t=\frac{1}{2}.1.5^2+1.10.1,25=25\)
Mình sửa xíu: Thế năng sau khi ném 0,5s:
\(W_t=mgh=10.1,25=12,5\)

a,\(\Rightarrow v^2=2gh\Rightarrow h=\dfrac{v^2}{2g}=\dfrac{20^2}{2.10}=20m\)
\(b,\Rightarrow v=gt\Rightarrow t=\dfrac{v}{g}=\dfrac{20}{10}=2s\)
c,\(\Rightarrow t=\sqrt{\dfrac{2,S'}{g}}=\sqrt[]{\dfrac{2.15}{10}}=\sqrt{3}\left(s\right)\)

a. \(v=\sqrt{2gh}=20\left(m/s\right)\)
b. Chọn mốc thế năng tại mặt đất O
Ta có: \(W_1=Wđ_1+Wt_1=mgz_1\) ( v1=0 => Wđ1= 0 )
Xét tổng quát cơ năng của vật tại vị trí động năng bằng n lần thế năng:
\(W_2=Wđ_2+Wt_2=nWt_2+Wt_2=\left(n+1\right)mgz2\)
Vật rơi tức là vật chịu tác dụng của trọng lực nên cơ năng được bảo toàn: \(W_1=W_2\)
\(\Leftrightarrow mgz_1=\left(n+1\right)mgz_2\)
áp dụng vào bài toán với n=1 ta được:
\(\Leftrightarrow z_2=\dfrac{z_1}{n+1}=\dfrac{20}{1+1}=10\left(m\right)\)
c. \(W_O=W_đ+W_t=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\left(\sqrt{2gh}\right)^2=mgh=20\left(J\right)\)