Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta\varphi=\omega\Delta t=2\left(rad\right)\) \(\Rightarrow\) \(\left\{{}\begin{matrix}\text{S}_{max}=2Asin\dfrac{\Delta\varphi}{\text{2}}=2.10sin1\approx\text{16,83(cm)}\\\text{S}_{\text{min}}=\text{2A}\left(\text{1-cos}\dfrac{\Delta\varphi}{\text{2}}\right)=2.10\left(\text{1-cos1}\right)\approx\text{9,19(cm)}\end{matrix}\right.\)
Tham khảo:
\(\Delta\varphi=\omega\Delta t=2\left(rad/s\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}S_{max}=2Asin\dfrac{\Delta\varphi}{2}=2\cdot10sin1\approx16,8\left(cm\right)\\S_{min}=2A\left(1-cos\dfrac{\Delta\varphi}{2}\right)=2\cdot10\cdot\left(1-cos1\right)\approx9,19\left(cm\right)\end{matrix}\right.\)

Tham khảo:
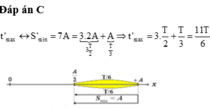
\(S_{max}=m\cdot2A+2Asin\dfrac{\Delta\varphi}{2}\Leftrightarrow12=1\cdot2\cdot4+4\)
\(\Rightarrow\left\{{}\begin{matrix}m=1\\\Delta\varphi=\dfrac{\pi}{3}\left(rad\right)\Rightarrow\Delta t=\dfrac{\Delta\varphi}{\dfrac{2\pi}{T}}=\dfrac{\dfrac{\pi}{3}}{\dfrac{2\pi}{T}}=\dfrac{T}{6}\end{matrix}\right.\)
Ta có: \(t=m\dfrac{T}{2}+\Delta t\Leftrightarrow2=1\cdot\dfrac{T}{2}+\dfrac{T}{6}\Rightarrow T=3\left(s\right)\)

Đáp án D
Trong khoảng thời gian t = T 4 thì vật có thể chuyển động từ vị trí ±A ® VTCB hoặc từ VTCB ® ±A hoặc từ vị trí
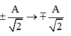

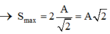

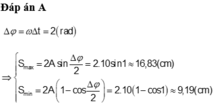
\(S=A\\ S'=A\)
Vậy quãng đường nhỏ nhất vật đi được trong T/3 bằng quãng đường lớn nhất vật đi được trong T/6.