Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời điểm đầu tiên vật đi qua li độ x = -12 cm là
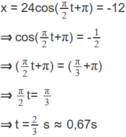
Tốc độ tại thời điểm t = 2/3s là:
v = - ω Asin( π /3 + π ) = 32,6 cm/s ≈ 33 cm/s

Thời điểm đầu tiên vật qua vị trí có li độ x = -12 cm

Tốc độ của vật tại thời điểm t = 2/3 s
![]()
⇒ v ≈ 0,33 m/s

Vận tốc cực đại khi vật qua vị trí cân bằng
Vật xuất phát tại M, đạt vận tốc có độ lớn cực đại lần đầu tiên ở N.
Thời gian: \(t=\dfrac{60+90}{360}T=\dfrac{5}{12}T\)

Đáp án D
Phương pháp:
- Áp dụng hệ thức độc lập với thời gian của vận tốc và li độ
- Sử dung̣ đường tròn lương̣ giác xác đinḥ pha ban đầu
Cách giải:
Ta có:
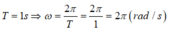
Ta sử dụng phương trình độc lập thời gian để tìm biên độ dao động:
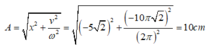
Tai thời điểm ban đầu vật ở vị trí x = - 5 2 và có vận tốc âm. Biểu diễn trên đường tròn lượng giác ta xác định được pha ban đầu của dao động là: φ = 3 π 4 rad
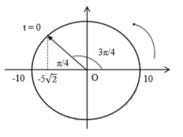
Khi đó ta có phương trình dao động là:
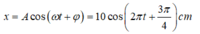

Viết phương trình dao động của vật
A = 24cm; T= 4s ⇒ ω = 2 π /T = π /2; Tại thời điểm ban đầu vật ở biên âm nên ta có φ = π
Nên phương trình dao động của vật là : x = 24cos( π t/2 + π ).

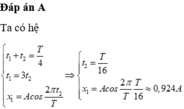
Tần số góc: \(\omega = \dfrac{2\pi}{T}=\dfrac{2\pi}{4}=0,5\pi(rad/s)\)
\(t=0\) khi vật ở \(x=-A\) \(\Rightarrow A\cos\varphi = -A\)
\(\Rightarrow \varphi = \pm\pi\)
Suy ra phương trình dao động: \(x=24\cos(0,5\pi t \pm\pi)\) (cm)
Để xác định thời điểm đầu tiên vật qua li độ x = -12cm, ta biểu diễn dao động bằng véc tơ quay:
Thời điểm đầu tiên vật qua x=-12cm ứng với véc tơ quay từ M đến N.
Thời gian: \(t=\dfrac{60}{360}T=\dfrac{60}{360}.4=\dfrac{2}{3}s\)
Tốc độ của vật được tính theo công thức độc lập: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 24^2=(-12)^2+\dfrac{v^2}{(0,5\pi)^2}\)
\(\Rightarrow v = 6\pi\sqrt 3\) (cm/s) (vận tốc lấy giá trị dương theo véc tơ quay như hình vẽ trên)