

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



ω=4π=>T=0,5s
\(\dfrac{t}{T}=\dfrac{5,75}{0,5}=11+0,5\)
tdư=0,5T=>α=π
khi t=0 có x0=2\(\sqrt{3}\) cm
Vẽ đường tròn thấy trong khoảng thời gian 0,5T vật không đi qua vị trí x=2 cm theo chiều dương lần nào cả
=> số lần vật đi qua vị trí x=2cm theo chiều dương trong 5,75s là 11 lần

Chọn D
+ T = 0,5s
+ t = 0: x = 2cos(-π/3) = 1cm ( x = A/2) và v = -8π sin(-π/3) = 4√3 cm/s > 0.
+ t = 0,125s: x = 2cos(4π. 0,125 - π/3) = √3cm (x = A√3/2) và v = -8π sin(4π. 0,125 - π/3) = -4π cm/s < 0.
+ Vì t = 0,125s < T nên vật sẽ đi từ vị trí A 2 → A → A 3 2 :
S = 1 + (4 - √3) = 1,27 cm.

Chọn gốc thời gian lúc vật ở vị trí 2,5√2 (em ghi sai chổ đó)

Chọn A
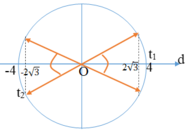
Khoảng cách giữa hai vật theo phương Ox là:
![]()
Theo bài ra ta có d ≥ 2√3
Trong khoảng t1 = 1/24 s đến t2 = 1/3s = t1 + T/2 +T/12, d có độ lớn không nhỏ hơn 2√3 trong khoảng thời gian là:
∆t = T/12 + 2. T/12 = 1/8s.

\(\dfrac{2}{3}T=\dfrac{T}{2}+\dfrac{T}{6}\)
+ Trong thời gian T/2 quãng đường vật đi được luôn là 2A (không có min, max)
+ Như vậy, ta cần tìm quãng đường nhỏ nhất trong thời gian T/6.
Biểu diễn dao động bằng véc tơ quay, trong thời gian T/6 thì véc tơ quay được góc là: 360/6 = 600.
Quãng đường nhỏ nhất khi vật đi tốc độ bé nhất --> Vật đi quanh vị trí biên.
\(\Rightarrow S_{min}=2.(A-A\cos 30^0)=2A(1-\cos 30^0)\)
Tổng quãng đường nhỏ nhất là: \(2A+2A(1-\cos 30^0)=2A(2-\cos 30^0)==2.4.(2-\cos 30^0)=9,07cm\)
Chọn đáp án C.