Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kì dao động của vật T = 2π/ω = 0,5s
Xét thời gian 7/48s = 7T/14 = T/8 + T/6
Ta có hình vẽ
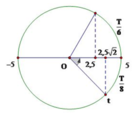
Từ hình vẽ ta thấy rằng, sau 7/48s vật đi qua vị trí có li độ x = 2,5 cm
Đáp án D

a/ \(4A=4.6=24\left(cm\right)\)
\(f=\frac{\omega}{2\pi}=\frac{4\pi}{2\pi}=2\left(Hz\right)\)
\(\varphi_0=\frac{\pi}{6}\left(rad\right)\)
b/ \(v=-\omega A\sin\left(\omega t+\varphi\right)=-4\pi.6.\sin\left(4\pi.\frac{1}{4}+\frac{\pi}{6}\right)=-4.\pi.6.\frac{-1}{2}=12\pi\left(cm/s\right)\)
\(a=-\omega.x=-4\pi.6\cos\left(4\pi.\frac{1}{4}+\frac{\pi}{6}\right)=-4\pi.6.\frac{-\sqrt{3}}{2}=12\sqrt{3}\pi\left(rad/s\right)\)
\(x=6.\cos\left(4\pi.\frac{1}{4}+\frac{\pi}{6}\right)=6.\frac{-\sqrt{3}}{2}=-3\sqrt{3}\left(cm\right)\)
d/ \(v_{max}=\omega A=4\pi.6=24\pi\left(cm/s\right)\)
\(a_{max}=\omega^2A=\left(4\pi\right)^2.6=96\pi^2\left(rad/s\right)\)

- Chọn D
- Ta có: x = -5cos(4πt) = 5cos(4πt + π)
Biên độ của dao động A = 5cm.
Pha ban đầu của dao động φ = π (rad).
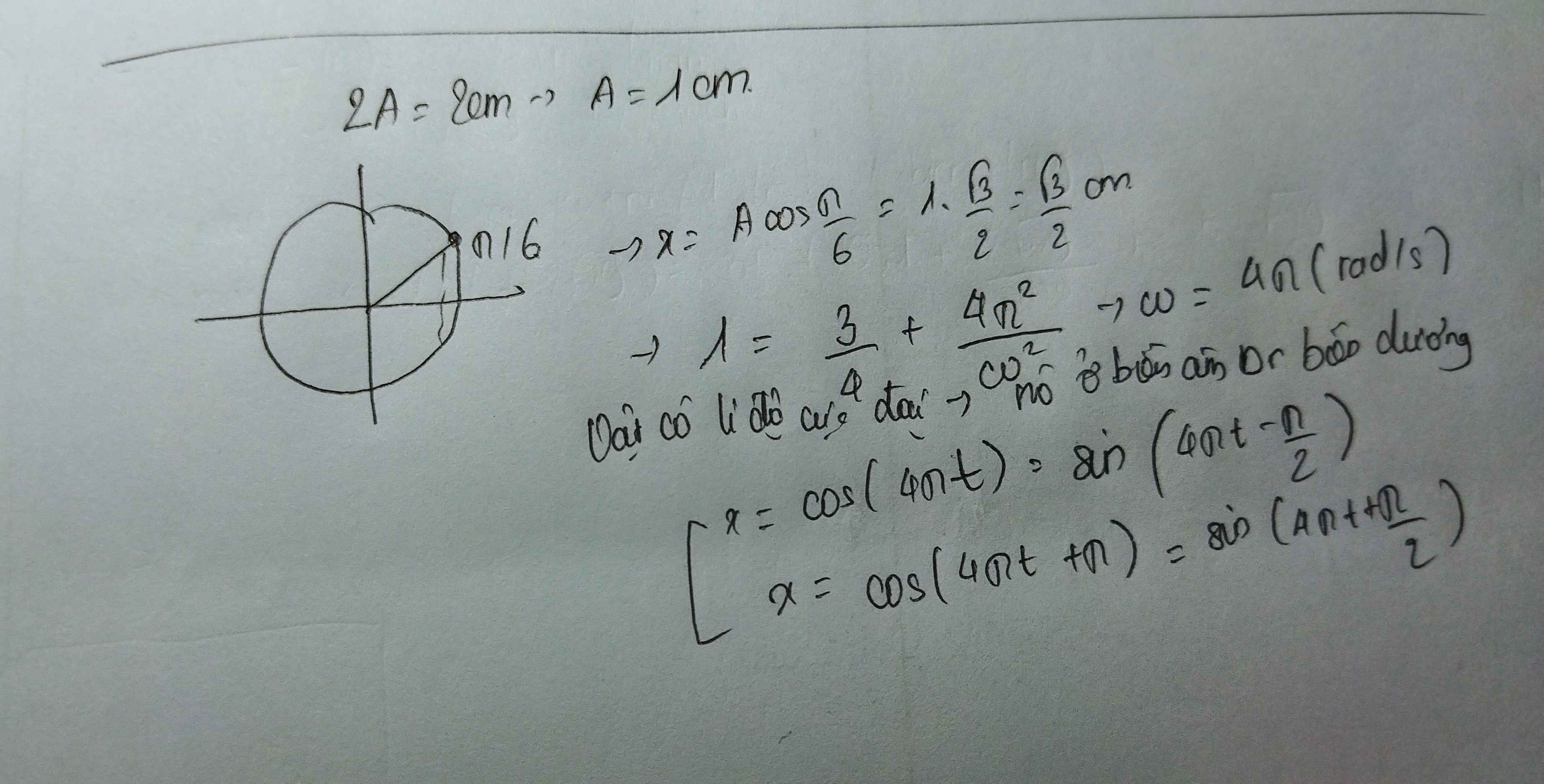
Chọn C
+ Phương trình dao động: x = Acos(ωt + φ).
+ Tìm các đại lượng:
* A: Có giá trị bằng một nửa quỹ đạo dài => A = 5 cm = 0,05m.
* ω: ω = 2πf = 4π rad/s.
* Tìm φ:
t = 0: v = -ωAsinφ < 0 => sinφ > 0 (1).
t = 2 (s): a = -ω2Acos(4πt + φ) = -ω2Acos(8π + φ) = -8cosφ = 4√3 m/s.
+ Thay vào các phương trình trên => x = 5cos(4πt +5π/6)(cm).