Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
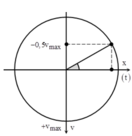
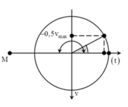
+ Tại thời điểm t vật ở xa M nhất tương ứng với vật đang ở biên dương. Sau Δt nhỏ nhất vật lại gần M nhất tương ứng với vị trí biên âm
→ Δt = 0,5T.
+ Vị trí vận tốc của vật có độ lớn bằng một nửa độ lớn cực đại ứng với vị trí M trên hình vẽ.
→ Ta dễ dàng xác định được t ' = t + Δt 6

\(T/4=0,15 \Rightarrow T=0,6s\)
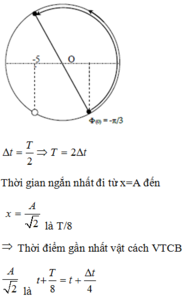
Áp dụng định luật bảo toàn năng lượng từ thời điểm khảo sát cho đến thời gian t:
\( W_đ+W_t = 3W_đ + \dfrac{W_t}{3} \Rightarrow \dfrac{2}{3}.W_t=2W_đ \Rightarrow W_t=3W_đ
\)\(\Rightarrow x_1=A.\dfrac{\sqrt{3}}{2} \Rightarrow x_2=\dfrac{A}{2}
\)
Suy ra thời gian chuyển động từ \(x_1\) đến \(x_2\) là \(\dfrac{T}{12}\)
\(\Rightarrow v_{tb}=\frac{S}{T/12}=73,2cm\)

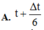
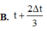
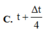
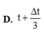



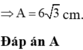
Đáp án D
+ Khoảng thời gian ngắn nhất để vật xa M nhất và gần M nhất là: