Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Sử dụng lí thuyết về dao động điều hoà
Pha dao động: (2πt + π/3)

Đáp án C
Phương pháp : Khoảng cách giữa hai vật ∆x = x1 – x2
Cách giải :
![]()
Vậy khoảng cách lớn nhất là 5,46cm

Đáp án C
Phương pháp: Áp dụng công thức tính vận tốc cực đại của vật dao động điều hoà v max = Aω
Vận tốc cực đại mà vật đạt được trong quá trình dao động là v max = Aω = 2 π . 4 = 8 π

Phương trình tổng quát: \(x= A\cos(\omega t +\varphi)\)
Áp dụng công thức độc lập: \(A^2 = x^2 +\frac{v^2}{\omega ^2} \Rightarrow (\frac{x}{A})^2+(\frac{v}{\omega A})^2=1\)\(\Rightarrow\left\{ \begin{array}{} A^2 = 16\ \\ \omega^2 A^2 =640 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} A = 4\ \\ \omega =2\pi \end{array} \right.\)
t = 0\(\Rightarrow\left\{ \begin{array}{} x_0 = A/2\\ v_0 <0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = \frac{1}{2}=0,5\\ \sin \varphi >0 \end{array} \right. \Rightarrow \varphi = \frac{\pi}{3}\)
Phương trình dao động: \(x=4\cos(2\pi t +\frac{\pi}{3}) \ (cm)\)

Chọn C
+ Hai dao động vuông pha: A = A 1 2 + A 2 2 = 8 2 ( c m )
+ Wđ = W – Wt = 1 2 mω2A2 - 1 2 mω2x2 = 1 2 mω2A2 - 1 2 mω2 ( A 2 ) 2
= 3 8 mω2A2 = 3 8 . 0,5.(2π)2. (8 2 .10-2) 2 = 0,096 J = 96mJ.

Chọn gốc thời gian lúc vật ở vị trí 2,5√2 (em ghi sai chổ đó)
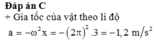
Chọn B
+ Đồng nhất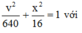
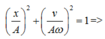
Từ đó: A = 4 (cm); ω = 2√10 = 2π rad/s.
+Tìm φ:
+ Thay vào biểu thức: x = 4cos(2πt + π/3) (cm)