Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Áp dụng định luật II Niuton ta có: mgsina - mmgcosa = ma
=> gsin300 - 0,1x.cos300 = a => 5 - 3 2 x = a = x ' '
+ Đặt:
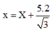
Ta có:
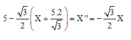
+ Phương trình trên có nghiệm là X = A cos ( 3 2 t + φ ) => v = - A 3 2 sin ( 3 2 t + φ )
+ Khi t = 0 thì v = 0 => j = 0 => v = - A 3 2 sin ( 3 2 t )
+ Khi dừng lại thì v = 0 => sin 3 2 t = 0 → t = 2 k π 3
+ Cho các giá trị của k và so đáp án ta được đáp án

Đáp án B
+ Áp dụng định luật II Niuton ta có: mgsina - mmgcosa = ma
=> gsin300 - 0,1x.cos300 = a => 5 - 3 2 x = a = x ' '
Đặt:

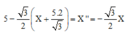
+ Phương trình trên có nghiệm là X = A cos ( 3 2 t + φ ) => v = - A 3 2 sin ( 3 2 t + φ )
+ Khi t = 0 thì v = 0 => j = 0 => v = - A 3 2 sin ( 3 2 t )
+ Khi dừng lại thì v = 0 => sin 3 2 t = 0 → t = 2 k π 3
+ Cho các giá trị của k và so đáp án ta được đáp án

- Nên nhớ các công thức trong dao động tắt dần:
- Quãng đường vật đi được đến khi dừng hẳn:
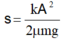
Thay số vào ta được:
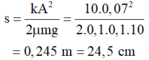

Đáp án B
Nên nhớ các công thức trong dao động tắt dần:
Quãng đường vật đi được đến khi dừng hẳn: s = k A 2 2 μ m g
Thay số vào ta được: s = 10 . 0 , 07 2 2 . 0 , 1 . 0 , 1 . 10 = 0 , 245 m = 24 , 5 c m

Chọn đáp án B
+ Sau 10 dao động vật dừng lại như vậy có 20 lần qua VTCB
+ Độ giảm biên độ của vật sau một lần qua VTCB:
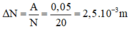
Mặt khác vật dao động tắt dần trên mặt phẳng nghiên nên ta có độ giảm biên độ sau một lần vật qua VTCB:
![]()

Chọn D
Độ biến dạng lò xo khi vật ở VTCB là
![]()
Ban đầu kéo vật đến vị trí lò xo giãn 18 cm → biên độ dao động của con lắc là A = 18 – 5 = 13 cm.
Áp dụng bảo toàn cơ năng ta có
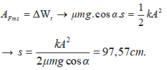
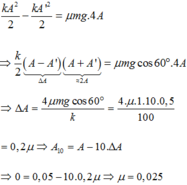

Theo định luật ll Niu tơn:
\(\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
Gia tốc vật:
\(a=-g\left(sin\alpha+k\cdot cos\alpha\right)\)
Quãng đường vật đi được:
\(S=\dfrac{-v_0^2}{2a}=\dfrac{-v_0^2}{2g\left(sin\alpha+k\cdot cos\alpha\right)}\)