Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi x là số sản phẩm làm 1 ngày theo dự định
3200/x là số ngày làm 3200 sp theo dự định
5+(3200-5x)/(x+40) là số ngày làm xong sản phẩm thực tê
ta có pt
3200/x-3=(5+(3200-5x)/(x+40))

Gọi số sản phẩm đội dự định làm mỗi ngày là x (x ∈ ℕ * , x < 84) (sản phẩm)
*) Theo kế hoạch, thời gian hoàn thành là 1000/x (ngày)
*) Thực tế, mỗi ngày làm được x + 10 (sản phẩm)
Thời gian hoàn thành 1000/(x+10) (ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
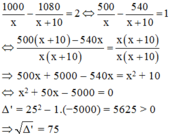
Phương trình có hai nghiệm phân biệt: x 1 = − 25 – 75 = −100 (loại)
và x 2 = −25 + 75 = 50 (tmđk)
Vậy theo kế hoạch, mỗi ngày tổ dự định làm 50 sản phẩm
Đáp án: C

Gọi số sản phẩm làm theo kế hoạch mỗi ngày là x>0 và số ngày dự định là y>0
Ta có: \(xy=200\)
4 ngày đầu làm được: \(4x\) sản phẩm
Những ngày còn lại: \(\left(y-6\right)\left(x+10\right)\)
Theo bài ra ta có hệ:
\(\left\{{}\begin{matrix}xy=200\\4x+\left(y-6\right)\left(x+10\right)=200\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=200\\5y-x=30\end{matrix}\right.\)
\(\Rightarrow y\left(5y-30\right)=200\)
\(\Leftrightarrow y^2-6y-40=0\Rightarrow\left[{}\begin{matrix}y=10\\y=-4\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{200}{10}=20\)

Gọi thời gian,năng xuất dự định lần lượt là x,y(x ngày,y sản phẩm)(x,y>0)
`=>` số sản phẩm dự định là `xy`
Nếu mỗi ngày tăng 5 sản phẩm thì sẽ hoàn thành trc 4 ngày
`=>xy=(x-4)(y+5)=xy-4y+5x-20`
`=>5x-4y=20(1)`
Nếu mỗi ngày giảm 5 sản phẩm thì hoàn thành chậm hơn 5 ngày
`=>xy=(x+5)(y-5)=xy+5y-5x-25`
`=>5y-5x=25(2)`
`(1)(2)` ta có hpt:
$\begin{cases}5x-4y=20\\5y-5x=25\end{cases}$
`<=>` $\begin{cases}y=45\\x=y-5=40\end{cases}$
`=>xy=1800`
Vậy thời gian làm theo dự định là 40 ngày và làm được 1800 sản phẩm
