Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có, lực kéo đàn hồi cần tác dụng lên đầu kia của thanh thép để thanh dài thêm 2,5 mm là: F d h = k . ∆ l = E S l 0 ∆ l = 2 . 10 11 1 , 5 . 10 - 4 5 2 , 5 . 10 - 3 = 15000 N
Đáp án: B
Ta có lực nén hay lực đàn hồi F = E S . Δ l l 0 ⇒ Δ l l 0 = F E S
Mà S = π d 2 4 = 3 , 14 ( 2.10 − 2 ) 2 4 = 3 , 14.10 − 4 ( m 2 )
⇒ Δ l l 0 = 1 , 57.10 5 2.10 11 .3 , 14.10 − 4 = 2 , 5.10 − 3
Vì hai bức tường cố định nên khoảng cách giữa chúng không đổi. Khi nhiệt độ tăng thì thanh xà nở dài thêm một đoạn ∆ l = 1,2 mm. Do đó, thanh xà tác dụng lên hai bức tường một lực có cường độ tính theo định luật Húc :
Độ nở dài tỉ đối của :
- Thanh thép khi bị nung nóng từ nhiệt độ t 1 đến t 2 :
- Thanh thép khi bị biến dạng kéo tính theo định luật Húc :
So sánh hai công thức này, ta tìm được lực do thanh thép tác dụng lên hai bức tường nếu nó bị nung nóng từ t 1 = 20 ° C đến t 2 = 200 ° C tính bằng :
Khi thanh dầm ngang bằng bê tông cốt thép chịu biến dạng uốn thì phần nửa phía dưới chịu biến dạng kéo dãn và phần nửa phía trên chịu biến dạng nén. Vì bê tông chịu nén tốt, nhưng chịu kéo dãn kém nên cần phải dùng các thanh thép làm cốt có đường kính lớn hơn và phải đặt chúng mau (dày) hơn trong phần nửa phía dưới của thanh dầm bê tông.
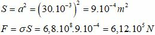
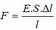
Ta có:
F = E S Δ l l 0 ⇒ F = 2.10 11 .2.10 − 4 . 1 , 5.10 − 3 4 ⇒ F = 15000 ( N )
Thanh thép có thể chịu đựng được các trọng lực nhỏ hơn Fb
P < F b = σ b S = 6 , 86.10 8 .2.10 − 4 ⇒ P < 137200 ( N )