Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp giải:
Tìm giá trị lớn nhất của thể tích khối nón và áp dụng công thức tính độ dài cùng tròn
Lời giải:
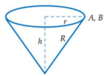
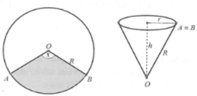
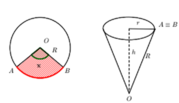
Gọi r, h lần lượt là bán kính đáy, chiều cao của phễu hình nón.
Thể tích của khối nón là 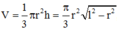 với l là độ dài đường sinh và l = R bán kính tấm bìa hình tròn =>
với l là độ dài đường sinh và l = R bán kính tấm bìa hình tròn => 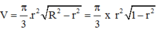 vì chuẩn hóa R = 1
vì chuẩn hóa R = 1
Xét hàm số ![]() trên (0;1) có
trên (0;1) có 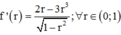
Ta có 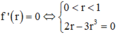
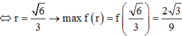
Do đó 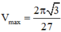 Dấu “=” xảy ra khi và chỉ khi
Dấu “=” xảy ra khi và chỉ khi 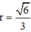
Mà độ dài cung phần cuộn làm phễu chính là chu vi đáy hình nón
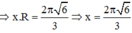

Dựa vào hình vẽ ta suy ra đáy của hình trụ có bán kính là h 2
Theo đề, ta có ![]()
=> h = 4 m
Suy ra kích thước của hình chữ nhật là 12 và 4 π
Diện tích của hình chữ nhật là ![]()
Chọn B.

Đáp án A.
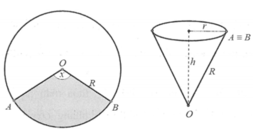
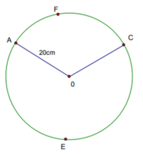
240 ° là 4 π 3 , Độ dài cung AEC là 20. 4 π 3 = 80 π 3 c m
Mà độ dài cung AEC là chu vi của đường tròn đáy nón nên ta có 80 π 3 = 2 π r ⇒ r= 40 3 là bán kính đường tròn đáy nón.
Diện tích xung quanh của nón là :
S x q = π 40 3 20 = 800 π 3 c m 2

Thể tích cái phễu là V = 1 3 πr 2 h
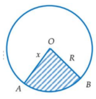
Ta có chu vi đáy là 2 πr = Rx
Suy ra
r = R x 2 π h = R 2 - r 2 = R 2 - R 2 x 2 4 π 2 = R 2 π 4 π 2 - x 2
Áp dụng bất đẳng thức AM-GM cho 2 số dương ta có:
V = 3 R 3 48 π 2 x 2 . 2 3 π 4 π 2 - x 2 ≤ 3 R 3 2 . 48 π 2 x 2 4 3 π 2 + 4 π 2 - x 2 = 3 R 3 2 . 48 π 2 x 2 16 3 π 2 - x 2 ≤ 1 8 3 R 3 48 π 2 . x 2 + 16 3 π 2 - x 2 2 = 1 8 3 R 3 48 π 2 . 16 2 9 π 4 = 2 3 27 πR 3
Dấu bằng có khi và chỉ khi
2 3 π = 4 π 2 - x 2 x 2 = 16 3 π 2 - x 2 ⇔ x = 2 2 3 π
Vậy 2 3 27 πR 3 khi và chỉ khi x = 2 2 3 πR 3
Đáp án A


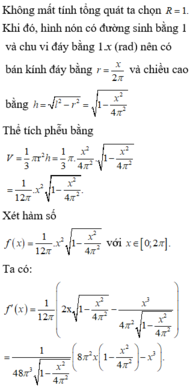

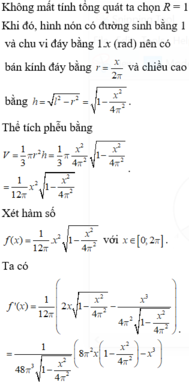




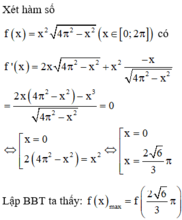
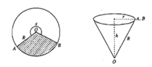
Chọn A.
Phương pháp:
+ Tính diện tích xung quanh hình nón còn lại
(với R là bán kính đáy hình nón, h là chiều cao hình nón và l là đường sinh hình nón)
Nhận xét rằng khi quấn hình quạt được cắt từ hình tròn thành hình nón thì đường sinh của hình nón chính là bán kính của hình tròn. Từ đó hình nón còn lại có đường sinh l = 5.
Lại có diện tích xung quanh hình nón còn lại là 10 π nên gọi R là bán kính hình nón này thì