Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án đúng D
Vì tốc độ truyền sóng chỉ phụ thuộc vào tính chất của môi trường như khối lượng riêng, nhiệt độ, độ đàn hồi của môi trường,... Nên khi thay đổi tần số dao động của nguồn sóng thì tốc độ truyền sóng không thay đổi.

Ta có: \(u=Acos\left(\dfrac{2\pi}{T}t+\dfrac{2\pi x}{\lambda}\right)\)
a, Có: \(\dfrac{2\pi}{T}=2\pi\Rightarrow T=1s\Rightarrow f=\dfrac{1}{T}=1\left(Hz\right)\)
Biên độ A = 10cm
b, Bước sóng: \(\dfrac{2\pi}{\lambda}=0,01\pi\Rightarrow\lambda=200cm\)
Tốc độ truyền sóng: \(v=\lambda f=200\cdot1=200\left(cm/s\right)\)
c, Ta có: \(u=10cos\left(2\pi\cdot4+0,01\pi\cdot50\right)=8,933cm\)

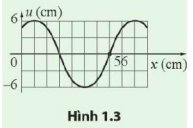
Biên độ sóng A = 6 cm
Ta thấy từ gốc x = 0 đến vị trí x = 56 có 7 khoảng, từ đó xác định được độ dài mỗi khoảng là 8 cm. Bước sóng ứng với 8 khoảng nên λ=64cm .

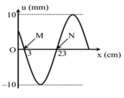
Điều kiện để xuất hiện sóng dừng trên dây có hai đầu cố định là L = \(n\frac{\lambda }{2}\)
Từ hình vẽ ta thấy trên dây xuất hiện 3 bụng sóng ⇒ n = 3
⇒ λ=\(\frac{{2L}}{n}\) = \(\frac{{2.1,2}}{3}\)= 0,8 (m)
Tốc độ sóng truyền trên dây là: v = λf = 0,8.13,3 = 10,64 (m/s)
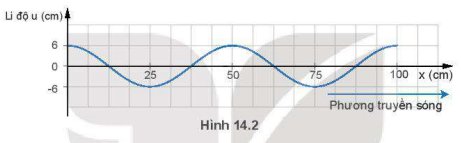

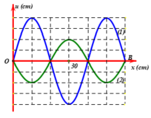


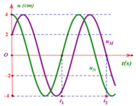

a) Từ đồ thị ta có bước sóng:
\(\lambda=50\left(cm\right)=0,5\left(m\right)\)
b) Chu kì 1s
\(\Rightarrow f=1Hz\)
Tốc độ truyền sóng:
\(v=\lambda f=0,5\cdot1=0,5\left(m/s\right)\)
c) Tần số tăng lên 5 Hz và tốc độ truyền sóng không đổi thì bước sóng mới là
\(\lambda_m=\dfrac{v}{f_m}=\dfrac{0,5}{5}=0,1\left(m\right)\)