Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Lời giải chi tiết:
Giả sử hai nguồn có phương trình dao động ![]()
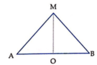
Gọi d là khoảng cách từ M tới 2 nguồn, phương trình sóng tại M là:
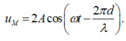
Phương trình sóng tại O là: 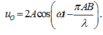
Độ lệch pha giữa chúng 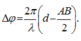
Để M và O cùng pha thì:
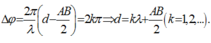
Vì M gần O nhất ứng với k=1
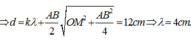
Tốc độ truyền sóng ![]()

Đáp án C
+ Độ lệch pha giữa hai điểm M và N:
∆ φ = 2 πdf v = ( 2 k + 1 ) π → f = ( 2 k + 1 ) v 2 d = 8 ( 2 k + 1 ) Hz
+ Với khoảng giá trị của tần số:
48 Hz ≤ f ≤ 64 Hz → f = 56 Hz .

+ Hai điểm M, N nằm trên cùng một phương truyền sóng dao động ngược pha nhau:
∆ φ = 2 π x λ = ( 2 k + 1 ) ⇔ 2 π f x v = ( 2 k + 1 ) π
⇒ f = ( 2 k + 1 ) v 2 x = 8 ( 2 k + 1 )
+ Với khoảng cách giá trị của f: 48 ≤ f ≤ 64
Sử dụng Mode → 7 ta tìm được f = 56 Hz
Chọn A

Đáp án B
HD: + Độ lệch pha giữa hai điểm M, N:

+ Với khoảng giá trị của tốc độ truyền sóng 70cm/s ≤ v ≤ 80 c m / s . Kết hợp với chức năng Mode → 7, ta tìm được v = 75 cm/s

+ Độ lệch pha giữa hai phần tử môi trường

Ghi chú: Ta có thể sử dụng chức năng lập bảng Table trên Casio bằng cách nhập lệnh Mode → 7 để xác định nhanh giá trị của vận tốc.
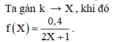
o Giá trị bắt đầu của : Start → tùy theo bài toán cụ thể, với bài toán trên ta có thể chọn giá trị bắt đầu của là 1.
o Giá trị kết thúc của : End → là giá trị cuối cùng của mà ta muốn tìm giá trị tương ứng của f(X)
o Bước nhảy của : Step → khoảng cách giữa hai giá trị liền kề của .
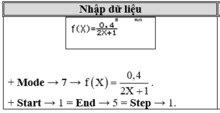

Đáp án D
+ Bước sóng của sóng λ = v f = 3 , 5 c m
Để H thuộc khoảng MN cùng pha với nguồn thì:
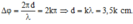
Với khoảng giá trị của d: 20 , 5 c m ≤ d ≤ 50 c m , sử dụng chức năng Mode → 7 ta tìm được 9 điểm cùng pha với O


Đáp án C
Hai điểm gần nhau nhất cách nhau ∆ d đồng pha khi: