Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Độ giãn của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 100 = 1 cm.
Tần số góc dao động của con lắc ω = k m = 10 10 rad/s.
+ Vận tốc truyền cho vật m so với điểm treo có độ lớn v 0 = 10 + 40 = 50 cm/s.
→ Biên độ dao động của vật sau đó A = v 0 ω = 50 10 10 = 1 , 58 cm.
→ Chiều dài cực đại l m a x = l 0 + Δ l 0 + A = 27 , 58 c m .

Đáp án A
+ Ta tính được
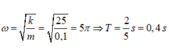
+ Độ biến dạng của lò xo khi vật ở vị trí cân bằng là
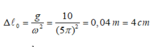
+ Từ VTCB, nâng vật lên 2 cm, tức là vật cách vị trí cân bằng 2 cm, suy ra |x| = 2 cm.
Áp dụng hệ thức liên hệ ta tính được biên độ dao động
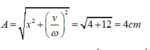
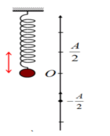
+ Sơ đồ chuyển động của vật được minh họa trên hình vẽ. Từ đó thay thấy thời điểm mà lúc vật qua vị trí lò xo dãn 6 cm lần hai (ở li độ x = 2 cm lần hai) là
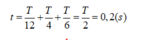

Đáp án C
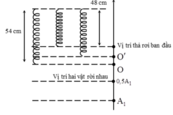

Tần số góc dao động điều hòa của hệ lò xo và hai vật ω = k 2 m = 100 2.0 , 2 = 5 10
→ Độ giãn của lò xo tại vị trí cân bằng Δ l 0 = g ω 2 = 4 c m
+ Từ vị trí cân bằng, nâng vật đến vị trí lò xo có chiều dài 48 cm rồi thả nhẹ →hai vật sẽ dao động với biên độ A 1 = 6 c m .
+ Phương trình động lực học cho vật m 2 trong quá trình vật chuyển động T – P 2 = m 2 a → tại vị trí vật m2 rời khỏi vật m 1 thì T = 3 , 5 N → m / s 2 (ta chú ý rằng gia tốc cực đại của dao động trên là a m a x = 15 m / s 2 ).
→ Tại vị trí m 2 rời khỏi vật m 1 , ta có x 0 = A 2 = 3 v 0 = 3 2 v m a x = 15 30
+ Sau khi m 2 rời khỏi m 1 , m 1 sẽ dao động điều hòa quanh vị trí cân bằng mới O' ở trên vị trí cân bằng cũ O một đoạn 2 cm → x 1 = 3 + 2 = 5 v 1 = v 0 = 15 30 , tần số dao động mới ω ' = k m = 100 0 , 2 = 10 5 rad/s
→ Biên độ dao động mới A 2 = 5 2 + 15 30 10 5 2 = 6 , 2 cm
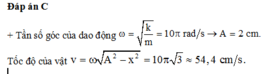


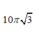
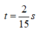
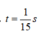

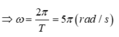
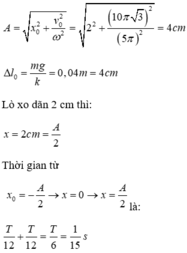
Chọn C