Một phân số có tử số bé hơn mẫu số là 13. Nếu tăng tử số lên 3 đơn vị và giảm mẫu số đi 4 đơn vị thì được một phân số bằ...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

J

jjhdjdjdj

25 tháng 3 2020

Một phân số có tử số bé hơn mẫu số là 13. Nếu tăng tử số lên 3 đơn vị và giảm mẫu số đi 4 đơn vị thì được một phân số bằng 3/4. Tìm phân số ban đầu

#Toán lớp 10

2

A

💋Amanda💋

25 tháng 3 2020

https://i.imgur.com/V5evFBI.jpg

TN

Thiện Nguyễn

25 tháng 3 2020

https://i.imgur.com/QEEH8xM.jpg

Các câu hỏi dưới đây có thể giống với câu hỏi trên

L

Loveduda

21 tháng 6 2017

1 phân số có tử bé hơn mẫu là 8. Nếu tăng tử số lên 3 đơn vị, giảm mẫu số đi 3 đơn vị thì phân số mới bằng 5/6. Tìm phân số ban đầu.

#Toán lớp 10

1

NH

Nguyễn Huy Tú

21 tháng 6 2017

Giải:

Gọi phân số cần tìm là \(\dfrac{a}{b}\)

Ta có: b = a + 8 và \(\dfrac{a+3}{b-3}=\dfrac{5}{6}\)

\(\Leftrightarrow6a+18=5b-15\)

\(\Leftrightarrow5b-6a=33\)

\(\Leftrightarrow5a+40-6a=33\)

\(\Leftrightarrow40-a=33\)

\(\Leftrightarrow a=7\Leftrightarrow b=15\)

Vậy phân số cần tìm là \(\dfrac{7}{15}\)

H

☘︎︎꧁ Hana_Love_ 花爱子シ꧂☘︎︎

28 tháng 2 2022

Tìm một phân số biết tổng của mẫu số và tử số là 99 đơn vị và phân số đó có giá trị bằng 51/136

#Toán lớp 10

1

NL

Nguyễn Lê Phước Thịnh

28 tháng 2 2022

Gọi tử là x

Mẫu là 99-x

Theo đề, ta có:

\(\dfrac{x}{99-x}=\dfrac{51}{136}=\dfrac{3}{8}\)

=>8x=297-3x

=>11x=297

=>x=17

Vậy: Phân só cần tìm là 17/82

KL

Khanh Lam

27 tháng 10 2021 - olm

xét tập tất cả phân số x/y trong đó x, y là các số nguyên dương nguyên tố cùng nhau hỏi có bao nhiêu phân số trong chúng có tính chất nếu cả tử và mẫu tăng lên 1 thì phân số đó tăng thêm 10%

#Toán lớp 10

0

QT

Quoc Tran Anh Le

Giáo viên

24 tháng 9 2023

Một mẫu số liệu có tử phân vị thứ nhất là 56 và tứ phân vị thứ ba là 84. Hãy kiểm tra xem trong hai giá trị 10 và 100 giá trị nào được xem là giá trị bất thường.

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

24 tháng 9 2023

Ta có \({Q_1} = 56;{Q_3} = 84\)

\({\Delta _Q} = {Q_3} - {Q_1} = 84 - 56 = 28\)

\({Q_1} - 1,5{\Delta _Q} = 56 - 1,5.28 = 14\)

\({Q_3} + 1,5.{\Delta _Q} = 84 - 1,5.28 = 126\)

Ta thấy 10 < 14 nên 10 là giá trị bất thường

QT

Quoc Tran Anh Le

Giáo viên

24 tháng 9 2023

Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:9 8 15 8 20b) Giá của một số loại giày (đơn vị nghìn đồng):350 300 650 300 450 500 300 250c) Số kênh được chiếu của một số hãng truyền hình cáp:36 38 33 34 32 30 34 ...

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

24 tháng 9 2023

a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:

9 8 15 8 20

Số trung bình: \(\overline X = \dfrac{{9 + 8 + 15 + 8 + 20}}{5} = 12\)

Trung vị:

Sắp xếp theo thứ tự không giảm:

8 8 9 15 20

Ta có n=5 là số lẻ nên trung vị là 9.

Mốt: Ta thấy số 8 là số có tần số cao nhất (xuất hiện 2 lần)

Tứ phân vị:

+ Tìm \({Q_2}\)

Ta có trung vị là 9=> \({Q_2} = 9\).

+ Tìm \({Q_1}\)

Nửa số liệu bên trái là:

8 8

Trung vị của mẫu này là \(\dfrac{{8 + 8}}{2} = 8\)=>\({Q_1} = 8\)

+ Tìm \({Q_3}\)

Nửa số liệu bên phải là:

15 20

Trung vị của mẫu này là \(\dfrac{{15 + 20}}{2} = 17,5\)=>\({Q_3} = 17,5\)

Vậy số trung bình là 12, trung vị là 9 và mốt là 8, \({Q_1} = 8\), \({Q_3} = 17,5\)

b) Giá của một số loại giày (đơn vị nghìn đồng):

350 300 650 300 450 500 300 250

Số trung bình: \(\overline X ) \( = \dfrac{{350 + 300.3 + 650 + 450 + 500 + 250}}{8}\) \( = 387,5\)

Trung vị:

Sắp xếp theo thứ tự không giảm:

250 300 300 300 350 450 500 650

Ta có n=8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.

Hai số chính giữa là 300 và 350

=> Trung vị là \(\dfrac{{300 + 350}}{2} = 325\)

Mốt: Ta thấy số 300 là số có tần số cao nhất (xuất hiện 3 lần)

Tứ phân vị:

+ Tìm \({Q_2}\)

Ta có trung vị là 325=> \({Q_2} = 325\).

+ Tìm \({Q_1}\)

Vì n chẵn nên nửa số liệu bên trái là:

250 300 300 300

Trung vị của mẫu này là \(\dfrac{{300 + 300}}{2} = 300\)=>\({Q_1} = 300\)

+ Tìm \({Q_3}\)

Vì n chẵn nên nửa số liệu bên phải là:

350 450 500 650

Trung vị của mẫu này là \(\dfrac{{450 + 500}}{2} = 475\)=>\({Q_3} = 475\)

Vậy số trung bình là 387,5, trung vị là 325 và mốt là 300, \({Q_1} = 300\), \({Q_3} = 475\)

c) Số kênh được chiếu của một số hãng truyền hình cáp:

36 38 33 34 32 30 34 35

Số trung bình: \(\overline X = \dfrac{{36 + 38 + 33 + 34.2 + 32 + 30 + 35}}{8} = 34\)

Trung vị:

Sắp xếp theo thứ tự không giảm:

30 32 33 34 34 35 36 38

Ta có n=8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.

Hai số chính giữa là 34 và 34

=> Trung vị là 34

Mốt: Ta thấy số 34 là số có tần số cao nhất (xuất hiện 2 lần)

Tứ phân vị:

+ Tìm \({Q_2}\)

Ta có trung vị là 34=> \({Q_2} = 34\).

+ Tìm \({Q_1}\)

Vì n chẵn nên nửa số liệu bên trái là:

30 32 33 34

Trung vị của mẫu này là \(\dfrac{{32 + 33}}{2} = 32,5\)=>\({Q_1} = 32,5\)

+ Tìm \({Q_3}\)

Vì n chẵn nên nửa số liệu bên phải là:

34 35 36 38

Trung vị của mẫu này là \(\dfrac{{35 + 36}}{2} = 35,5\)=>\({Q_3} = 35,5\)

Vậy số trung bình là 34, trung vị là 34 và mốt là 34, \({Q_1} = 32,5\), \({Q_3} = 35,5\)

Chú ý

Nếu n chẵn thì nửa số liệu bên trái (phải) \({Q_2}\) phải chứa cả \({Q_2}\)

F

fghfghf

9 tháng 11 2016

Tìm số có ba chữ số, biết rằng chữ số hàng trăm gấp 4 lần chữ số hàng đơn vị và nếu viết số ấy theo thứ tự ngược lại thì nó giảm đi 594 đơn vị.

#Toán lớp 10

1

DQ

Đặng Quỳnh Ngân

9 tháng 11 2016

http://olm.vn/hoi-dap/question/646913.html

PT

Pham Trong Bach

28 tháng 8 2019

Thống kê điểm toán của 40 học sinh của một lớp người ta thu được mẫu số liệu ban đầu như sau: Lập bảng phân bố tần số - tần suất ghép lớp với các lớp như sau: [1; 2]; [3; 4]; [5; 6]; [7; 8]; [9; 10] Hỏi có mấy lớp có tần suất không bé hơn 17,5% A. 1 B. 2 C. 3...

#Toán lớp 10

1

CM

Cao Minh Tâm

28 tháng 8 2019

Chọn C.

Bảng phân bố tần số - tần suất

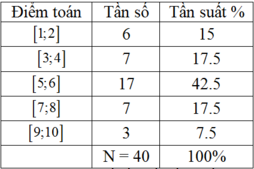
Dựa vào bảng phân bố tần số; tần suất trên ta thấy có 3 lớp có tần suất không bé hơn 17,5% là lớp thứ 2;3 và lớp thứ 4.

PT

Pham Trong Bach

24 tháng 5 2018

Điều tra về số tiền mua sách trong một năm của 40 sinh viên ta có mẫu số liệu sau (đơn vị nghìn đồng): Các số liệu trên được phân thành 10 lớp: L 1 = [ 0 ; 100 ) , L 2 = [ 100 ; 200 ) , . . . , L 10 = [ 900 ; 1000 ) a) c) Có khoảng bao nhiêu phần trăm số sinh viên có mức cho cho việc mua sách từ 500 nghìn...

#Toán lớp 10

1

CM

Cao Minh Tâm

24 tháng 5 2018

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:

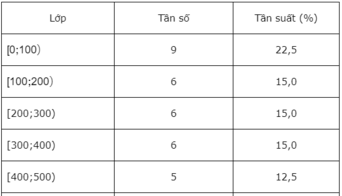
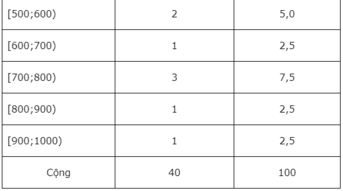
c) Cộng các tần suất của năm lớp [500;600), [600;700), [700;800), [800;900) và [900;1000) ta được . Đáp án là B.

PT

Pham Trong Bach

11 tháng 6 2018

Một số có ba chữ số. Nếu lấy số đó chia cho tổng các chữ số của nó thì được thương là 17 và dư 5. Nếu đổi hai chữ số hàng chục và hàng trăm cho nhau thì được số mới mà chia cho tổng các chữ số của nó thì được thương là 30 và dư là 4. Nếu đổi hai chữ số hàng chục và hàng đơn vị của số mới này cho nhau thì được một số mà chia cho tổng các chữ số của nó thì được...

#Toán lớp 10

1

CM

Cao Minh Tâm

11 tháng 6 2018

Gọi ba chữ số của số đó theo thứ tự hàng trăm, hàng chục, hàng đơn vị là a, b, c (0 < a ≤ 9; 0 ≤ b, c ≤ 9). Ta được hệ phương trình

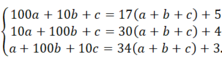
Giải sách bài tập Toán 10 | Giải sbt Toán 10

Giải hệ phương trình này tốn nhiều thời gian, không đáp ứng yêu cầu của một bài trắc nghiệm.

Do đó ta phải xét các phương án

- Với phương án A, tổng các chữ số là 10, do đó chia 172 cho 10 được thương là 17 và dư là 2 nên phương án A bị loại.

- Với phương án B, tổng các chữ số là 17. Đổi chữ số hàng trăm cho chữ số hàng chục ta được số 926, số này chia cho 17 không thể có thương là 30, nên phương án B bị loại.

- Với phương án D, nếu đổi chữ số hàng trăm với chữ số hàng chục ta được 857, chia số này cho tổng các chữ số là 20 không thể có thương là 34 nên phương án D bị loại.

Đáp án: C