Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp giải:
Dựa vào đồ thị hàm số xác định hoành độ điểm D suy ra tung độ điểm A chính là độ dài BC
Lời giải: Gọi ![]() với
với ![]()
Gọi ![]() thuộc đồ thị
thuộc đồ thị ![]()
Vì ABCDlà hình chữ nhật ![]()
Khi đó BC = m. Mà ![]()
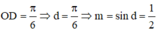

Đáp án B
Gọi R,h lần lượt là bán kính đáy và chiều cao của khối trụ ⇒ h = 6 R = 6 . Thể tích của khối trụ là V = πR 2 h = π . 1 2 . 6 = 6 π . Khối cầu bên trong khối trụ có bán kính là R = 1 ⇒ V C = 4 3 π . R 3 = 4 3 π . Khối nón bên trong khối trụ có bán kính đáy là R = 1 và chiều cao h - 2R = 4. Suy ra thể tích khối nón là V N = 1 3 πR 2 h = 1 3 . π . 1 2 . 4 = 4 3 π . Do đó, thể tích lượng nước còn lại bên trong khối trụ là V 0 = V - V C + V N = 6 π - 2 . 4 π 3 = 10 π 3 . Vậy tỉ số cần tính là T = V 0 V = 10 π 3 : 6 π = 5 9 .

Đáp án A.
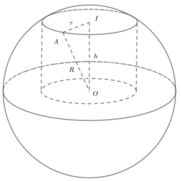
Gọi I là tâm của đường tròn dáy của chỏm cầu. M là 1 đỉnh của hình hộp thuộc đường tròn I ; R 2 .
Ta có:
I M = R 2 ; O M = R ⇒ O I = R 2 − R 2 4 = 3 R 2 .
Do đó khối hộp có chiều cao là
h = 3 R = 10 3 .
Thể tích của chỏm cầu bị cắt:
V = ∫ h 2 R π R 2 − x 2 d x = ∫ 5 3 10 π 100 − x 2 d x ≃ 53 , 87.
Thể tích của khối hộp chữ nhật:
V = S d . h = R 2 2 . 3 . R = 3 2 R 3 ≃ 866 , 025.
Thể tích khối cầu ban đầu:
V = 4 3 π R 3 ≃ 4188 , 79.
Do đó thể tích cần tính:
V ≃ 4188 , 79 − 866 , 025 − 2.53 , 87 ≃ 3215 , 023.

Chọn C.
Phương pháp:
Công thức tính diện tích mặt cầu bán kính R là: S = 4 π R 2 .
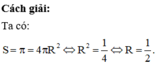

Chọn C.
Phương pháp: Dựa vào dữ kiện bài toán lập hàm số và tìm giá trị lớn nhất, nhỏ nhất.

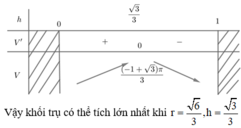
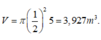
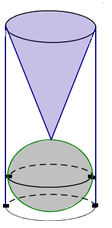






Ta xem hình cầu được sinh bởi khi quay hình tròn (C): x + y = a quanh Oy và hình trụ sinh bởi phần mặt phẳng của hai đường thẳng x = 0; x = a 2 quay quanh Oy.
Ta có y 2 = a 2 - x 2 ⇒ y = ± a 2 - x 2 .
Thể tích cần tìm là:
V = 4 π ∫ a 2 a x a 2 - x 2 dx = - 2 π ∫ a 2 a a 2 - x 2 d a 2 - x 2 = - 4 π 3 a 2 - x 2 3 2 a 2 a = π 3 2 a 3
Đáp án A