Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc xe máy là x (km/h). Thì vận tốc ô tô là: \(x+10\)(km/h).
Thời gian để xe máy đi hết AB là: \(\frac{120}{x}\)(h)
Thời gian để ô tô đi hết AB là : \(\frac{120}{x+10}\)
\(\Rightarrow\frac{120}{x}-\frac{120}{x+10}=\frac{36}{60}=0,6\)
\(\Leftrightarrow\hept{\begin{cases}x=-50\left(l\right)\\x=40\end{cases}}\)
Vậy vận tốc xe máy là 40 (km/h) vận tốc ô tô là: 50(km/h).
p/s : kham khảo

Gọi vận tốc xe máy là x (km/h). Điều kiện x>0
Do vận tốc xe ô tô lớn hơn vận tốc xe máy là 10km/h nên vận tốc ô tô là x+10 (km/h).
Thời gian xe máy đi từ A đến B là 120 x (h)
Thời gian ô tô đi từ A đến B là 120 x + 10 (h)
Xe ô tô đến B sớm hơn xe máy 36 phút =3/5(h) nên ta có phương trình:
120 x − 120 x + 10 = 3 5 ⇔ 120.5. x + 10 − 120.5. x = 3 x . x + 10 ⇔ 3 x 2 + 30 x − 6000 = 0 ⇔ x + 50 x − 40 = 0 ⇔ x = − 50 x = 40
Kết hợp với điều kiện đầu bài ta được x= 40.
Vậy vận tốc của xe máy là 40 (km/h), vận tốc của ô tô là 50(km/h).

Gọi vận tốc xe máy là x (km/h). Thì vận tốc ô tô là: \(x+10\)(km/h).
Thời gian để xe máy đi hết AB là: \(\frac{120}{x}\)(h)
Thời gian để ô tô đi hết AB là: \(\frac{120}{x+10}\)
\(\Rightarrow\frac{120}{x}-\frac{120}{x+10}=\frac{36}{60}=0,6\)
\(\Leftrightarrow\hept{\begin{cases}x=-50\left(l\right)\\x=40\end{cases}}\)
Vậy vận tốc xe máy là 40 (km/h) vận tốc ô tô là: 50(km/h).

Gọi vận tốc xe máy là x
=>Vận tốc ô tô là x+10
Theo đề, ta có: 60/x-60/x+10=3/10
=>20/x-20/x+10=1/10
=>(20x+200-20x)/(x^2+10x)=1/10
=>x^2+10x-2000=0
=>x=40
=>V ô tô=50km/h

Gọi vận tốc xe máy là x (km/h). Điều kiện: x > 0
Gọi vận tốc ô tô là y (km/h). Điều kiện: y > 0
Thời gian xe máy dự định đi từ A đến B là: 210/x giờ
Thời gian ô tô dự định đi từ B đến A là: 210/y giờ
Quãng đường xe máy đi được kể từ khi gặp ô tô cho đến khi đến B là: 4x (km)
Quãng đường ô tô đi được kể từ khi gặp xe máy cho đến khi đến A là: 9/4 (km)
Theo giả thiết ta có hệ phương trình:
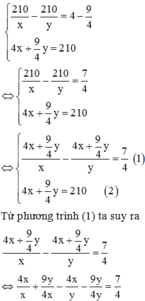

Đáp án B

thời gian mà xe máy đi được là: `9h30-7h=2,5h`
thời gian mà ô tô đi được là: `2,5h-1h=1,5h`
gọi vận tốc của xe máy là: x (đơn vị: km/h; x>0)
=> vận tốc của ô tô là: `x+20`(km/h)
quãng đường mà xe máy đi được là: `2,5x`(km)
quãng đường mà ô tô đi được là: `1,5(x+20)` (km)
vì quãng đường mà hai xe đi được bằng tổng độ dài quãng đường AB là 190km nên ta có phương trình sau
`2,5x+1,5(x+20)=190`
`<=>2,5x+1,5x+30=190`
`<=>4x=160`
`<=>x=40(tm)`
vậy vận tốc của xe máy là: 40(km/h)
vận tốc của ô tô là: `40+20=60`(km/h)
Đổi thời gian mà xe máy đi được là: 9h30−7h=2,5h
thời gian mà ô tô đi được là: 2,5h−1h=1,5h
Gọi vận tốc của xe máy là: x (đơn vị: km/h; x>0)
=> vận tốc của ô tô là: x+20 (km/h)
Quãng đường mà xe máy đi được là: 2,5x (km)
Quãng đường mà ô tô đi được là: 1,5(x+20) (km)
Vì quãng đường mà hai xe đi được bằng tổng độ dài quãng đường AB là 190km nên ta có phương trình sau
2,5x+1,5(x+20)=190
⇔2,5x+1,5x+30=190
⇔4x=160
⇔x=40(tm)
Vậy vận tốc của xe máy là: 40(km/h)
vận tốc của ô tô là: 40+20=60(km/h)
Vận tốc của ô tô là v, vận tốc của xe máy là m.
Theo đề bài, vận tốc của ô tô lớn hơn vận tốc của xe máy là 20km/h.
Ta có thể đặt thời gian đi của ô tô là t và thời gian đi của xe máy là t + 0.5 (30 phút = 0.5 giờ).
Vận tốc của ô tô là v = 60 / t và vận tốc của xe máy là m = 60 / (t + 0.5).
Vận tốc của ô tô lớn hơn vận tốc của xe máy 20km/h, ta có phương trình:
v - m = 20.
Thay v = 60 / t và m = 60 / (t + 0.5) vào phương trình trên, ta có:
60 / t - 60 / (t + 0.5) = 20.
Giải phương trình trên, ta có thể tính được giá trị của t. Sau đó, thay t vào công thức v = 60 / t và m = 60 / (t + 0.5), ta có thể tính được vận tốc của mỗi xe.
Gọi \(v_1;v_2\) lần lượt là vận tốc của ô tô và xe máy (km/h)
\(t\) là thời gian xe ô tô đi đến AB
Ta có :
\(\left\{{}\begin{matrix}v_1=\dfrac{s}{t}=\dfrac{60}{t}\left(1\right)\\v_2=\dfrac{s}{t}=\dfrac{60}{t+0,5}\left(2\right)\end{matrix}\right.\)
mà \(v_1-v_2=20\)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{60}{t}-\dfrac{60}{t+0,5}=20\)
\(\Leftrightarrow60\left(\dfrac{1}{t}-\dfrac{1}{t+0,5}\right)=20\)
\(\Leftrightarrow3.\dfrac{0,5}{t\left(t+0,5\right)}=1\)
\(\Leftrightarrow t\left(t+\dfrac{1}{2}\right)=\dfrac{3}{2}\)
\(\Leftrightarrow t^2+\dfrac{t}{2}=\dfrac{3}{2}\)
\(\Leftrightarrow2t^2+t-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=1\\t=-\dfrac{3}{2}\left(loại\right)\end{matrix}\right.\) \(\Leftrightarrow t=1\)
\(\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{60}{1}=60\\v_2=60-20=40\end{matrix}\right.\) (km/h)