Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(36\left(\dfrac{km}{h}\right)=10\left(\dfrac{m}{s}\right)-54\left(\dfrac{km}{h}\right)=15\left(\dfrac{m}{s}\right)\)
\(t=\dfrac{v-v_0}{a}=\dfrac{15-10}{0,1}=50\left(s\right)\)
Ta có: \(v^2-v^2_0=2aS\)
\(=>S=\dfrac{v^2-v_0^2}{2a}=\dfrac{15^2-10^2}{2\cdot0,1}=625\left(m\right)\)
Vậy.............................

Ô tô đang chuyển động với vận tốc v0 = 36 km/h = 10 m/s thì xuống dốc và chuyển động thẳng nhanh dần đều với gia tốc a = 0,2 m/ s 2 . Do đó quãng đường ô tô đi được trong khoảng thời gian t là được tính theo công thức s = v 0 t + (a t 2 )/2, thay số vào ta được
960 = 10t + (0.2 t 2 )/2 ⇔ t 2 + 100t − 9600 = 0
Do đó giải được t = 60 s.

Vận tốc của ô tô ở cuối đoạn dốc là
v = v 0 + at = 10 + 0,2.60 = 22 (m/s) = 79,2 (km/h)

7,2km/h = 2 m/s
72km/h = 20 m/s
Chọn chiều dương là chiều lên dốc, gốc tọa độ tại chân dốc, ta có :
Phương trình tọa độ của xe ô tô là:
x = 20.t + 0,4.t²/2 = 20t + 0,2t² (1)
Phương trình tọa độ của xe đạp là:
x' = 570 - 2.t - 0,2.t²/2 = 570 - 2t - 0,1t² (2) ( lấy v < 0 và a < 0 do nó có hướng ngược chiều dương )
Hai xe gặp nhau khi x = x'
=> 20t + 0,2t² = 570 - 2t - 0,1t²
<=> 0,3t² + 22t - 570 = 0
∆' = 11² - 0,3.(- 570) = 292
=> t = 20,3 (s)
=> x = 20.20,3 + 0,2.(20,3)² = 488,4 (m)
Vậy hai xe gặp nhau lúc t = 20,3 (s) và cách chân dốc x = 488,4 (m)
b)
Quãng đường ô tô đi được khi gặp nhau là:
s2 = x = 488,4 (m)
Vận tốc ô tô lúc đó là:
v2 = vo2 + at = 20 + 0,4.20,3 = 28,12 (m/s)
Quãng đường xe đạp đi được khi gặp nhau là:
s1 = 570 - 488,4 = 81,6 (m)
Vận tốc xe đạp lúc đó là:
v1 = vo1 + at = 2 + 0,2.20,3 = 6,06 (m/s)
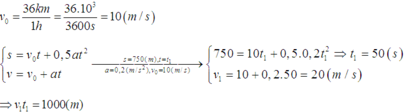

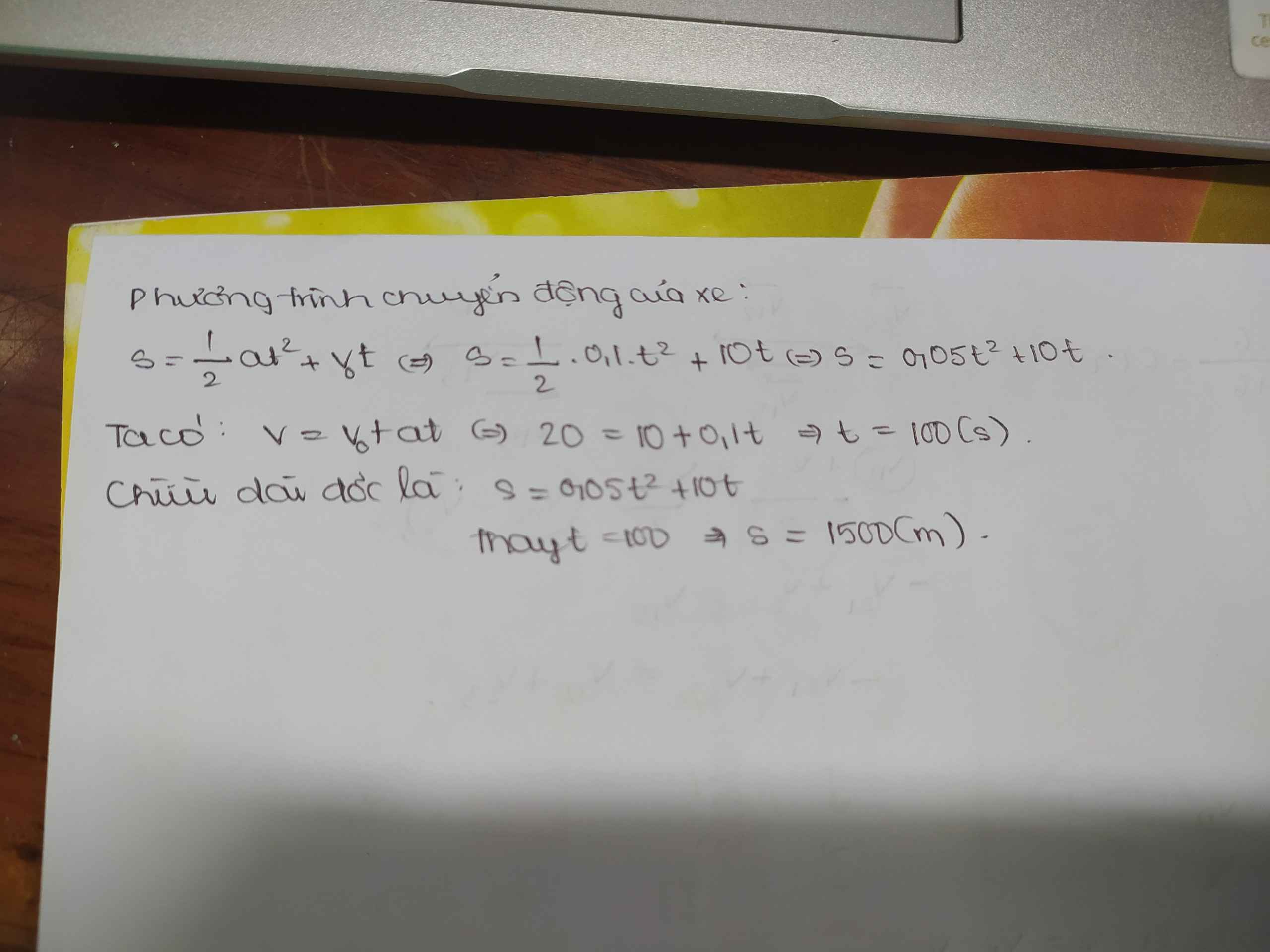
\(v_0=36km/h=10m/s\)
\(a=0,1m/s^2\)
\(v=72km/h=20m/s\)
____________________________
a) s =?; t =?
GIẢI :
a) \(v^2-v_0^2=2as\)
=> \(s=\frac{v^2-v_0^2}{2a}=\frac{20^2-10^2}{2.0,1}=1500\left(m\right)\)
Thời gian xe đi hết dốc:
\(t=\frac{v-v_0}{a}=100\left(s\right)\)
đổi 36km/h = 10m/s, 54km/h = 15m/s
ta có: 2as = v^2 - v0^2
<=> s = (15^2 - 10^2) / 2* 0.1 = 625
T = (v - v0 )/a = (15 -10)/ 0.1 = 50s