Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Tính độ lớn gia tốc
Áp dụng công thức a = F/m = 600/1600 = 0,375(m/ s 2 )
* Véc tơ gia tốc cùng hướng với lực hãm phanh, nghĩa là ngược hướng với hướng chuyển động ban đầu

Độ lớn gia tốc mà lực hãm phanh gây ra cho xe là
a = F/m = 600/1600 = 0,375 (m/ s 2 )
Hướng của gia tốc trùng với hướng của lực, tức là ngược với hướng của chuyển động.

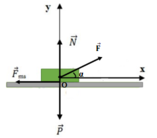
a) Các lực tác dụng lên vật được biểu diễn như hình vẽ. Chọn hệ trục Ox theo hướng chuyển động, Oy vuông góc phương chuyển động.
Áp dụng định luật II Niu – tơn ta được:
![]()
Chiếu hệ thức vecto lên trục Ox ta được:
Fcosα - Fms = ma (1)
Chiếu hệ thức vecto lên trục Oy ta được:
Fsinα - P + N = 0 ⇔ N = P - Fsinα (2)
Mặt khác Fms = μtN = μt(P - Fsinα) (3)
Từ (1) và (2) (3) suy ra:
![]()
b) Để vật chuyển động thẳng đều (a = 0) ta có:
![]()
⇔ Fcosα - μt(P - Fsinα) ⇒ F = 12(N)

Ta có
\(s_1+s_2=\dfrac{v_1^2}{2a_1}+\dfrac{-v_1^2}{2a_2}=\dfrac{v_1^2}{2\cdot2}+\dfrac{-v_1^2}{2\cdot\left(-2,5\right)}=180\Rightarrow v_1=20\left(\dfrac{m}{s}\right)\)
Quãng đường chuyển động của xe trong từng giai đoạn
\(s_1=\dfrac{v_1^2}{2\cdot a_1}=\dfrac{20^2}{2\cdot2}=100\left(m\right);s_2=\dfrac{-v_1^2}{2\cdot a_2}=-\dfrac{20^2}{2\cdot\left(-2,5\right)}=80\left(m\right)\)
Thời gian qua từng giai đoạn
\(t_1=\sqrt{\dfrac{2s_1}{a_1}}=10\left(s\right);t_2=\sqrt{\dfrac{2s_2}{a_2}}=8\left(s\right)\)


Chọn D.
Chọn chiều dương là chiều chuyển động.
Từ : a = F ht m = - 400 1600 = - 0 , 25 ( m / s 2 ) .