Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Quãng đường vật ô tô đi được trong 5 giây là
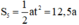
Quãng đường ô tô đi được trong 4 giây là:
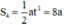
Quãng đường ô tô đi đươc trong giây thứ 5 là:

Sao giây thứ 4 lại là 8a, trong đề bài có cho đâu, trong lời giải bạn cũng đâu có tính, vậy 8a đó đâu ra?

Ta có: \(\left\{{}\begin{matrix}v=v_0+at\\S=v_0t+\dfrac{1}{2}at^2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}0=v_0+a\cdot5\\3,125=v_0\cdot5+\dfrac{1}{2}\cdot a\cdot5^2\end{matrix}\right.\)
\(\Rightarrow\) \(v_0=1,25\)m/s và \(a=-0,25\) m/s2

Ta có
\(s_1+s_2=\dfrac{v_1^2}{2a_1}+\dfrac{-v_1^2}{2a_2}=\dfrac{v_1^2}{2\cdot2}+\dfrac{-v_1^2}{2\cdot\left(-2,5\right)}=180\Rightarrow v_1=20\left(\dfrac{m}{s}\right)\)
Quãng đường chuyển động của xe trong từng giai đoạn
\(s_1=\dfrac{v_1^2}{2\cdot a_1}=\dfrac{20^2}{2\cdot2}=100\left(m\right);s_2=\dfrac{-v_1^2}{2\cdot a_2}=-\dfrac{20^2}{2\cdot\left(-2,5\right)}=80\left(m\right)\)
Thời gian qua từng giai đoạn
\(t_1=\sqrt{\dfrac{2s_1}{a_1}}=10\left(s\right);t_2=\sqrt{\dfrac{2s_2}{a_2}}=8\left(s\right)\)

Giải:
Chọn chiều dương là chiều chuyển động của ô tô, gốc tọa độ tại vị trí uống nước, gốc thời gian là lúc xe ô tô khởi hành.
Đối với xe ô tô

Đáp án A.
Xét bài toán tổng quát: Một vật chuyển động thẳng chậm dần đều với gia tốc a. Tính quãng đường vật đi được trong n giây cuối trước khi vật dừng hẳn.
Giả sử chọn chiều dương là chiều chuyển động của vật. Gốc thời gian là lúc vật bắt đầu chuyển động.
Gọi t là thời gian để vật đi toàn bộ quãng đường s đến khi vật dừng hẳn thì:
Quãng đường vật đi được trong ( t – n ) giây đầu là:
Vậy quãng đường vật đi được trong n giây cuối cùng trước khi dừng hẳn là:
Mà khi vật dừng lại thì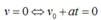
Vậy ta có
Lưu ý: Do ∆ s >0 nên a<0 , phù hợp với tính chất của chuyển động chậm dần đều khi chọn chiều dương là chiều chuyển động thì .
Khi vật chuyển động chậm dần đều, quãng đường vật đi được trong n giây cuối trước khi vật dừng hẳn là:
Áp dụng vào bài toán: