Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 20 phút = 1/3 giờ ; 30 phút = 1/2 giờ; 15 phút = 1/4 giờ ;
Vận tốc xe trên đoạn AB là :
12 : 1/3 = 36 (km/giờ)
Vận tốc xe trên đoạn đường BC là :
12 : 1/2 = 24 (km/giờ)
Vận tốc xe trên đoạn đường CD là :
12 : 1/4 = 48 (km/giờ)
Vận tốc của xe trên cả đoạn đường là :
(36 + 24 + 48) : 3 = 36 (km/giờ)
Áp dụng công thức Vtb=\(\frac{\Delta x}{\Delta t}\) ta có:
+ Trên đoạn đường AB: Vtb=\(\frac{12000}{20.60}=10m\) / s
+ Trên đoạn đường BC: Vtb=\(\frac{12000}{30.60}=6,67m\) / s
+ Trên đoạn đường CD: Vtb=\(\frac{12000}{20.60}=10m\) / s
+ Trên đoạn đường AD: Vtb=\(\frac{12000.3}{\left(20+30+20\right).60}=8,57m\) / s

Áp dụng công thức : vtb = \(\frac{\triangle x}{\triangle t}\) ta có :
+ Trên đoạn đường AB : vtb = \(\frac{12000}{20.600}=10\)m / s
+ Trên đoạn đường BC : vtb = \(\frac{12000}{30.60}\) = 6,67 m / s
+ Trên đoạn đường CD : vtb = \(\frac{12000}{20.60}\) = 10 m / s
+ Trên đoạn đường AD : vtb = \(\frac{12000.3}{\left(20+30+20\right).60}\) = 8,57 m /s
Không thể biết chắc chắn sau 40 min kể từ khi xe qua A , xe ở vị trí nào vì ta không biết được tính chất của chuyển động trên mỗi đoạn.

\(v_{AB}=\dfrac{s_{AB}}{t_{AB}}=\dfrac{10}{5}=2\left(\dfrac{m}{s}\right)\)
\(v_{BC}=\dfrac{s_{BC}}{t_{BC}}=\dfrac{20}{2}=10\left(\dfrac{m}{s}\right)\)
\(v_{CD}=\dfrac{s_{CD}}{t_{CD}}=\dfrac{40}{10}=4\left(\dfrac{m}{s}\right)\)
\(v_{AD}=\dfrac{s_{AB}+s_{BC}+s_{CD}}{t_{AB}+t_{BC}+t_{CD}}=\dfrac{10+20+40}{5+2+10}=\dfrac{70}{17}\left(\dfrac{m}{s}\right)\)

+ Do nửa đầu của khoảng thời gian đó xe chạy với tốc độ v 1 = 60 km/s ⇒ quãng đường đi được là s 1 = v 1 .t/2 = 30t
+ Do nửa cuối của khoảng thời gian đó xe chạy với tốc độ v 2 = 40 km/h ⇒ quãng đường đi được là s 2 = v 2 .t/2 = 20t
⇒ Độ dài quãng đường AB là s = s1 + s2 = 50t
⇒ Tốc độ trung bình trên cả quãng đường AB là v t b = 50t/t = 50 km/h

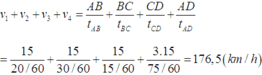
bạn kéo xuống nhé, mik giải câu này rồi