Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nl nhôm toả ra là
\(Q_{tỏa}=0,4.880\left(120-50\right)=24640J\)
Ta có pt cân bằng nhiệt
\(Q_{tỏa}=Q_{thu}\\ \Leftrightarrow24640=2.4200\left(50-t\right)\\ \Rightarrow t=47^o\)

Tóm tắt:
\(m_1=0,5kg\\ m_2=4kg\\ m_3=0,2kg\\ t_1=20^0C\\ t_2=500^0C\\ c_1=896J/kg.K\\ c_2=4180J/kg.K\\ c_3=460J/kg.K\)
____________
\(t=?^0C\)
Giải
Nhiệt độ của hỗn hợp sau khi cân bằng là:
Theo pt cân bằng nhiệt:
\(Q_1+Q_2=Q_3\\ \Leftrightarrow m_1.c_1.\left(t-t_1\right)+m_2.c_2.\left(t-t_1\right)=m_3.c_3.\left(t_2-t\right)\\ \Leftrightarrow0,5.896.\left(t-20\right)+4.4200.\left(t-20\right)=0,2..460.\left(500-t\right)\\ \Leftrightarrow t\approx22,6^0C\)

Đáp án: C
- Nhiệt lượng cần cung cấp cho 1,6kg nước đá thu vào để tăng nhiệt độ từ - 10 0 C lên 0 0 C :
![]()
- Nhiệt lượng nước đá thu vào để nóng chảy hoàn hoàn ở 0 0 C
![]()
- Nhiệt lượng do 2kg nước toả ra để hạ nhiệt độ từ 50 0 C đến 0 0 C
![]()
- Nhiệt lượng do nhiệt lượng kế bằng nhôm toả ra để hạ nhiệt độ từ 80 0 C xuống tới 0 0 C
![]()
- Ta có:
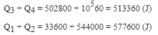
![]()
- Vì Q t h u > Q toả chứng tỏ nước đá chưa tan hết
- Nhiệt độ cuối cùng của hỗn hợp nước và nước đá cũng chính là nhiệt độ cuối cùng của nhiệt lượng kế và bằng 0 0 C

Gọi m1 là khối lượng của chì, m2 là khối lượng của kẽm, m là khối lượng của hợp kim:
m = m1 + m2 = 0,05kg (1)
Nhiệt lượng chì và kẽm tỏa ra:
Q1 = m1.c1.(t0 - t) = m1.130.(136 – 18) = 15340.m1
Q2 = m2.c2.(t0 - t) = m2.210.(136 – 18) = 24780.m2
Nhiệt lượng nước thu vào:
Qn = mn.cn.(t - tn) = 0,05.4200.(18 - 14) = 810J
Vì muốn cho nhiệt lượng kế nóng thêm lên 1oC thì cần 65,1J nên nhiệt lượng kế thu vào:
Q4 = Qk.(t – tn) = 65,1.(18 – 14) = 260,4J
Vì nhiệt lượng tỏa ra bằng nhiệt lượng thu vào nên: Q3 + Q4 = Q1 + Q2
↔ 15340.m1 + 24780.m2 = 1100,4 (2)
Từ (1), rút m2 = 0,05 – m1, thay vào phương trình (2), giải ra ta được:
m1 = 0,015kg, suy ra m2 = 0,035kg
Vậy khối lượng chì là 15 gam và khối lượng kẽm là 35 gam.

Nhiệt lượng nhôm tỏa ra:
\(Q_1=m_1c_1\left(t_1-t\right)=0,4\cdot880\cdot\left(120-50\right)=24640J\)
Gọi nhiệt độ ban đầu của nước là \(t_2^oC\)
Nhiệt lượng nước thu vào:
\(Q_2=m_2c_2\left(t-t_2\right)=2\cdot4200\cdot\left(50-t_2\right)\)
Cân bằng nhiệt: \(Q_1=Q_2\)
\(\Rightarrow24640=2\cdot4200\cdot\left(50-t_2\right)\)
\(\Rightarrow t_2=47,07^oC\)

m1 = 100g = 0,1kg ; c1 = 900J/g.K ; t1 = 10oC
m2 = 400g = 0,4kg ; c2 = 4200J/kg.K
m = 200g = 0,2kg ; c3 = 230Jkg.K ;
Gọi khối lượng phần nhôm và phần thiếc trong thỏi hợp kim là mn và mt. Ta có:
\(m_n+m_t=m\Rightarrow m_t=m-m_n\left(1\right)\)
Nhiệt lượng do thỏi hợp kim tỏa ra khi hị nhiệt từ t2 = 120oC xuống t3 = 14oC là:
\(Q_{tỏa}=\left(m_n.c_1+m_t.c_3\right)\left(t_2-t_3\right)\\ =\left(900m_n+230m_t\right)\left(120-14\right)=10600\left(9m_n+2,3m_t\right)\)
Nhiệt lượng mà nước và nhiệt lượng kế nhôm thu vào để tăng nhiệt độ từ t1 = 10oC đến t3 = 14oC là:
\(Q_{thu}=\left(m_1.c_1+m_2.c_2\right)\left(t_3-t_1\right)=\left(0,1.880+0,4.4200\right)\left(14-10\right)=7072\left(J\right)\)
Thep phương trình cân bằng nhiệt:
\(Q_{tỏa}=Q_{thu}\\ \Rightarrow10600\left(9m_n+2,3m_t\right)=7072\\ \Rightarrow9m_n+2,3m_t=\dfrac{7072}{10600}\left(2\right)\)
Thay (1) vào (2):
\(9\left(m-m_t\right)+2,3m_t=\dfrac{7072}{10600}\\ \Rightarrow9m-9m_t+2,3m_t=\dfrac{7072}{10600}\\ \Rightarrow9m-m_t\left(2,3-9\right)=\dfrac{7072}{10600}\\ \Rightarrow-m_t=\dfrac{\dfrac{7070}{10600}-9.0,2}{2,3-9}\\ \Rightarrow m_t\approx0,16908\left(g\right)\\ \Rightarrow m_n=0,03092\left(g\right)\)
Phần nhôm có khối lượng 30,92kg phần thiếc có khối lượng 169,08kg.

Tóm tắt:
\(m_1=100g\)
\(m_2=40g\)
\(c_1=90J\)/kg.K
\(c_2=4200J\)/kg.K
\(t_1=10^0C\)
_______________
\(m_3=?kg\)
\(m_2=?kg\)
Giải:
Nhiệt lượng hợp kim tỏa ra là:
\(Q_t=\left(m_3.c_3+m_4.c_4\right).t\)
= \(\left(900.m_3+230.m_4\right)\left(120-14\right)\)
= \(160.\left(900m_3+230m_3\right)\)
Nhiệt lượng của nhiệt kế nước nhôm
\(Q_{th}=\left(m_1.c_1+m_2.c_2\right)\Delta t\)
=\(\left(0,1.900+0,4.4200\right)\left(14-10\right)\)
=7800J
Khi cân bằng là:
\(Q_t=Q_{th}\)
\(\Rightarrow106\left(900m_3+230m_4\right)=7080\)
\(\Rightarrow53.900m_3+230.53m_4=3540\)
ta có \(m_3+m_4=0,2\)
giải phương trình Ta được:
\(\Rightarrow\left\{{}\begin{matrix}m_3=0,03\left(kg\right)\\m_4=0,17\left(kg\right)\end{matrix}\right.\)
Vậy:................................