

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



+ Gọi I là một điểm bất kì nằm trêm MN. Để đơn giản, ta chọn λ = 1
Độ lệch pha dao động giữa nguồn và I là:

→ có 1 điểm.
→ Trên MN sẽ có 6 điểm dao động ngược pha với nguồn.
→ Đáp án B
Chú ý: Ở bài này ta không xác định trực tiếp số điểm cực pha với nguồn trên MN dựa vào khoảng giá trị O N ≤ d ≤ O M vì sự lặp lại cùng một giá trị của d

Đáp án C
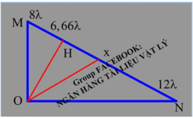
+ Gọi OH là đường cao kẻ từ O đến MN.
+ Ta có: 1 O H 2 = 1 O M 2 + 1 O N 2 = 1 8 λ 2 + 1 12 λ 2
⇒ O H ≈ 6 , 66 λ
+ Những điểm dao động ngược pha với O thỏa mãn điều kiện: x = k + 0 , 5 λ
+ Đi từ H đến M có 1 điểm 7 , 5 λ
+ Đi từ H đến N có 7 , 5 λ ; 8 , 5 λ ; 9 , 5 λ ; 10 , 5 λ ; 11 , 5 λ
+ Vậy tổng trên MN có 6 điểm dao động ngược pha với O.
Chú ý: Cách giải này cũng áp dụng cho các loại bài cùng hoặc lệch pha bất kì

Đáp án B
Điểm dao động cùng pha với nguồn O thì phải cách nguồn đoạn là d=k λ
H là điểm trên MN gần nguồn O nhất có: 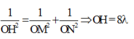
Số điểm cùng pha với nguồn trên MH thỏa mãn bất phương trình
![]() Vậy có 3 điểm kể cả H và M.
Vậy có 3 điểm kể cả H và M.
Số điểm cùng pha với nguồn trên NH thỏa mãn bất phương trình
![]()
Vậy có 5 điểm không kể điểm H.
Như vậy tổng có tất cả 8 điểm trên MN dao động cùng pha với nguồn O.

Đáp án C
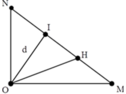
+ Gọi I là một điểm bất kì nằm trên MN
Độ lệch pha dao động giữa nguồn và I là: ∆ φ = 2 π d λ = ( 2 k + 1 ) π ⇒ d = ( 2 k + 1 ) λ 2
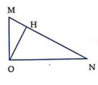
+ Gọi H là trung điểm của MN, khi đó dựa vào tính chất của tam giác vuông ta có O H = M N 2 = 2 13 λ
+ Số điểm dao động ngược pha với O trên đoạn NH:
2 13 λ ≤ ( 2 k + 1 ) λ 2 ≤ 12 λ ⇒ 6 , 7 ≤ k ≤ 12 , 5 → Có 5 điểm.
+ Số điểm dao động ngược pha với O trên đoạn MH: 2 13 λ ≤ ( 2 k + 1 ) λ 2 ≤ 8 λ ⇒ 6 , 7 ≤ k ≤ 7 , 5 → Có 1 điểm.
Vậy có tất cả 6 điểm dao động ngược pha với O trên đoạn MN.

Gọi \(I\) là điểm bất kì trên MN.
Độ lệch pha: \(\Delta\varphi=\dfrac{2\pi d}{\lambda}=\left(2k+1\right)\pi\)
\(\Rightarrow d=\left(2k+1\right)\dfrac{\lambda}{2}\)
Gọi H là trung điểm MN.
\(\Rightarrow OH=\dfrac{MN}{2}=2\sqrt{13}\lambda\)
Số dao động ngược pha:
+Trên MH: \(2\sqrt{13}\lambda\le\left(2k+1\right)\dfrac{\lambda}{2}\le8\lambda\Rightarrow6,7\le k\le7,5\)
\(\Rightarrow\) Có 1 điểm
+Trên NH: \(2\sqrt{13}\lambda\le\left(2k+1\right)\dfrac{\lambda}{2}\le12\lambda\Rightarrow6,7\le k\le12,5\)
\(\Rightarrow\) Có 5 điểm
Vậy có tất cả 6 điểm thỏa mãn

Đáp án C
+ Đường kính của đường tròn d = 2R = 8λ.
Các điểm cùng pha với O nằm trên các đường tròn cách nhau một khoảng λ.
+ Xét tỉ số d/ λ=8 => trên đường tròn có 15 điểm cùng pha với O