Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số tiền gửi ban đầu là A thì số tiền người đó thu về (cả gốc và lãi) sau n năm là A ( 1 + 0 , 061 ) n và số tiền lãi người đó thu về là A ( 1 + 0 , 061 ) n - A
Ta cần tìm n nhỏ nhất sao cho
A ( 1 + 0 , 061 ) n - A ≥ A ⇔ 1 , 061 n ≥ 2 ⇔ n ≥ log 1 , 061 2 ≈ 11 , 7062
Vậy sau ít nhất 12 năm người này sẽ thu về số tiền lãi ít nhất bằng số tiền ban đầu.
Chọn đáp án A.

Chọn đáp án D.
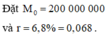
Gọi M n là số tiền cả gốc và lãi thu được sau n năm gửi tiết kiệm.
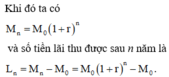
Để dùng tiền lãi mua được chiếc xe máy giá 47 990 000 đồng thì
Dáp án D là chính xác !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Đáp án C
Gọi n là số năm cần gửi, suy ra 100 1 + 7 % n ≥ 250 ⇔ n ≥ 13,54 ⇒ n = 14

Đáp án A
Phương pháp:
Công thức lãi kép: T = M 1 + r n với:
T là số tiền cả vốn lẫn lãi sau n kì hạn;M là số tiền gửi ban đầu; n là số kỳ hạn; r là lãi suất định kỳ, tính theo %.
Cách giải: Gọi n là số năm cần gửi ít nhất để người đó có 250 triệu.
Ta có: 250.10 6 = 100.10 6 1 + 7 , 4 n
⇔ n = log 1 + 7 , 4 % 250.10 6 100.10 6 ≈ 12 , 8 ⇒ n = 13 (năm).
Chú ý khi giải: HS sẽ phân vân khi chọn số năm cần gửi ít nhất vì n ~ 12 , 8 nên có thể sẽ chọn đáp án sai là n=12.

Đáp án C
Theo công thức lãi kép ta có T = A 1 + r n trong đó
T là cả tiền gốc lẫn lãi khi lấy về
A là số tiền ban đầu
R là lãi suất
N là số kỳ hạn
Khi đó 250 = 100 1 + 7 100 n ⇒ n = log 1 , 07 250 100 ≈ 13 , 54 năm.
Để người đó lãnh được số tiền 250 triệu thì người đó cần gửi trong khoảng thời gian 14 năm

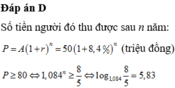
Chọn C
Gọi A là số tiền gửi ban đầu, n là số năm gửi.
Theo bài ra: Sau 1 năm, số tiền cả vốn lẫn lãi là : A + A. 8,4% =A. 1,084.
Sau 2 năm, số tiền cả vốn lẫn lãi là: A.1,084 + A. 1,084.8,4% = A. 1,084^2.
Sau n năm, số tiền cả vốn lẫn lãi là A. 1,084^n.
Số tiền này bằng 2 lần ban đầu nên: A. 1,084^n = 3A
ð n = ~ 14