Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.


Gọi B là số tiền của người đó trong tài khoản tiết kiệm đến hết tháng 12 năm 2020. Khi đó n = 24
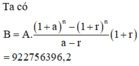

Chọn đáp án C.
Gọi M là số tiền ban đầu; r là lãi suất hàng tháng.
Số tiền lãi tháng 1 là
Số tiền cả vốn lẫn lãi tháng 1 là M(1+r)
Số tiền còn lại sau khi chuyển cho Lâm m đồng là M(1+r) - m
Tương tự: Số tiền còn lại sau tháng thứ 2 là:

Vì sau 48 tháng là hết tiền trong tài khoản nên ta có:
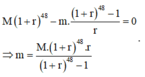
![]()



Đáp án C.
Gọi M là số tiền ban đầu; r là lãi suất hàng tháng.
Số tiền lãi tháng 1 là M.r.
Số tiền cả vốn lẫn lãi tháng 1 là M(1+r).
Số tiền còn lại sau khi chuyển cho Lâm m đồng là M 1 + r − m .
Tương tự: Số tiền còn lại sau tháng thứ 2 là:
M 1 + r − m 1 + r − m = M 1 + r 2 − m 1 + r + 1
Số tiền còn lại sau tháng thứ 3 là:
M 1 + r 2 − m 1 + r + 1 1 + r − m = M 1 + r 3 − m 1 + r 2 + 1 + r + 1
= M 1 + r 3 − m . 1 + r 3 − 1 1 + r − 1 = M 1 + r 3 − m . 1 + r 3 − 1 r
…
Số tiền còn lại sau 48 tháng là: M 1 + r 48 − m . 1 + r 48 − 1 r .
Vì sau 48 tháng là hết tiền trong tài khoản nên ta có:
M 1 + r 48 − m . 1 + r 48 − 1 r = 0 ⇒ m = M . 1 + r 48 . r 1 + r 48 − 1
Thay số vào ta tìm được m ≈ 4.920.224 (đồng).

Gửi lần đầu thu về tổng số tiền 100 1 + 0 , 02 4 gửi lần kế tiếp thu về 100 1 + 0 , 02 2
Tổng số tiền nhận được sau đúng 1 năm kể từ lần gửi đầu tiên là
100 1 + 0 , 02 4 + 100 1 + 0 , 02 2 ≈ 212 . 283 . 000
đồng.
Chọn đáp án A.

Áp dụng công thức lãi kép ![]() với A số tiền gửi vào lần đầu tiên, r = 0,55% là lãi suất mỗi tháng, n = 23 tháng và Tn = 50.000.000 đồng. Ta được
với A số tiền gửi vào lần đầu tiên, r = 0,55% là lãi suất mỗi tháng, n = 23 tháng và Tn = 50.000.000 đồng. Ta được
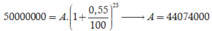 đồng. Chọn D.
đồng. Chọn D.

Đáp án D
Số tiền người đó nhận được sau 6 tháng từ ngân hang là: 100 1 + 0,05 2 = 110,25 triệu đồng
Sau 1 năm người đó nhận được số tiền từ ngân hàng là 110,25 + 50 1 + 0,05 2 = 176,676 triệu đồng


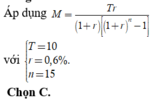
Đáp án D
Gọi A là số tiền ban đầu mà người đó gửi vào ngân hàng.
Sau 1 tháng số tiền người đó nhận được là A 1 + r
Sau 2 tháng số tiền người đó nhận được là A 1 + r 2
…
Sau n tháng số tiền người đó nhận được là A 1 + r n
Giả sử sau n tháng, số tiền trong tài khoản của người đó gấp n lần số tiền ban đầu. Ta có 4 A = A 1 + r n
⇔ 4 = 1 + 0 , 01 n
⇔ n = log 1 , 01 4 ≈ 140 .
Vậy sau 140 tháng thì số tiền của người đó trong tài khoản gấp 4 lần số tiền ban đầu.