Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ \(AH\perp BD\Rightarrow BD\perp\left(SAH\right)\Rightarrow\widehat{SHA}\) là góc giữa (SBD) và (ABCD)
\(\frac{1}{AH^2}=\frac{1}{AD^2}+\frac{1}{AB^2}\Rightarrow AH=\frac{AB.AD}{\sqrt{AB^2+AD^2}}=\frac{a\sqrt{3}}{2}\)
\(SA=\sqrt{SD^2-AD^2}=2a\)
\(tan\widehat{SHA}=\frac{SA}{AH}=\frac{4\sqrt{3}}{3}\Rightarrow\widehat{SHA}\simeq66^035'\)
b/ \(MS=MA\Rightarrow d\left(S;\left(MND\right)\right)=d\left(A;\left(MND\right)\right)\)
Từ A kẻ \(AK\perp MD\Rightarrow AK\perp\left(MND\right)\Rightarrow AK=d\left(A;\left(MND\right)\right)\)
\(AM=\frac{SA}{2}=a\Rightarrow\frac{1}{AK^2}=\frac{1}{AM^2}+\frac{1}{AD^2}\Rightarrow AK=\frac{AM.AD}{\sqrt{AM^2+AD^2}}=\frac{a\sqrt{3}}{2}\)

Chọn A
Chọn 1 nam trong 20 học sinh nam có C 20 1 cách.
Chọn 1 nữ trong 15 học sinh nữ có C 15 1 cách.
Áp dụng quy tắc nhân có : C 20 1 . C 15 1 = 300 cách.

Đáp án C
Xếp ngẫu nhiên học sinh thành một hàng có 10! ⇒ n ( Ω ) = 10 !
Gọi biến cố A : “Xếp học sinh thành một hàng sao cho An và Bình đứng cạnh nhau”.
Xem An và Bình là nhóm X .
Xếp X và học sinh còn lại có 9! cách.
Hoán vị An và Bình trong X có 2! cách.

Chọn C
Số cách chọn 3 người từ một nhóm 12 người là: C 12 3

Đáp án : B
Để chọn một bút chì - một bút bi - một quyển sách , ta có:
Có 9 cách chọn bút chì.
Có 5 cách chọn bút bi.
Có 10 cách chọn cuốn tập.
Vậy theo qui tắc nhân ta có 9.5.10=450 cách.

Chọn C
Số phần tử của không gian mẫu là: ![]() .
.
Gọi biến cố A: “ Hai người được chọn đều là nam”.
![]()
Vậy xác suất cần tìm là: 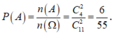 .
.